题目内容
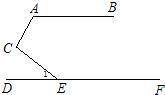
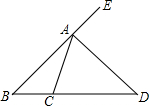
如图,AD是∠CAE的平分线,∠B=45°,∠DAE=75°,则∠ACD为( )
| A.105° | B.85° | C.60° | D.75° |

∵AD是△ABC的外角∠CAE的平分线,∠B=45°,∠DAE=75°,
∴∠EAC=2∠DAE=2×75°=150°,
∵∠EAC是△ABC的外角,
∴∠EAC=∠B+∠ACB,
∵∠B=45°,
∴∠ACB=∠EAC-∠B=150°-45°=105°,
∴∠ACD=180°-∠ACB=180°-105°=75°.
故选D.
∴∠EAC=2∠DAE=2×75°=150°,
∵∠EAC是△ABC的外角,
∴∠EAC=∠B+∠ACB,
∵∠B=45°,
∴∠ACB=∠EAC-∠B=150°-45°=105°,
∴∠ACD=180°-∠ACB=180°-105°=75°.
故选D.

练习册系列答案
相关题目