题目内容
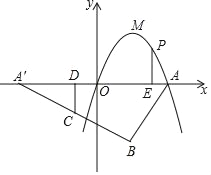
【题目】抛物线y=ax2+bx的顶点M(![]() ,3)关于x轴的对称点为B,点A为抛物线与x轴的一个交点,点A关于原点O的对称点为A′;已知C为A′B的中点,P为抛物线上一动点,作CD⊥x轴,PE⊥x轴,垂足分别为D,E.
,3)关于x轴的对称点为B,点A为抛物线与x轴的一个交点,点A关于原点O的对称点为A′;已知C为A′B的中点,P为抛物线上一动点,作CD⊥x轴,PE⊥x轴,垂足分别为D,E.
(1)求点A的坐标及抛物线的解析式;
(2)当0<x<2![]() 时,是否存在点P使以点C,D,P,E为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
时,是否存在点P使以点C,D,P,E为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2+2![]() x(2)存在点P(
x(2)存在点P(![]() +
+![]() ,
,![]() )或(
)或(![]() ﹣
﹣![]() ,
,![]() )使得四边形CDPE是平行四边形
)使得四边形CDPE是平行四边形
【解析】
(1)由抛物线的对称性质求得点A的坐标,然后分别将点A、O的坐标代入函数解析式,列出关于a,b的方程组,通过解方程组求得它们的值即可;
(2)假设存在点P使得以点C,D,P,E为顶点的四边形是平行四边形,则PE∥CD且PE=CD.根据点的对称性质可得BF=3,结合三角形中位线定理求得PE=![]() .根据x的取值范围确定点P应该在x轴的上方.可设点P的坐标为(x,
.根据x的取值范围确定点P应该在x轴的上方.可设点P的坐标为(x,![]() ),利用二次函数图象上点的坐标特征进行解答.
),利用二次函数图象上点的坐标特征进行解答.
(1)依题意得:抛物线y=ax2+bx经过顶点M(![]() ,3)和(0,0),∴点A与原点关于对称轴x=
,3)和(0,0),∴点A与原点关于对称轴x=![]() 对称,∴A(2
对称,∴A(2![]() ,0),∴
,0),∴![]() ,解得:
,解得:![]() ,∴抛物线的解析式为:y=﹣x2+2
,∴抛物线的解析式为:y=﹣x2+2![]() x;
x;
(2)假设存在点P使得以点C,D,P,E为顶点的四边形是平行四边形,则PE∥CD且PE=CD.
由顶点M(![]() ,3)关于x轴的对称点B(
,3)关于x轴的对称点B(![]() ,﹣3),可得:BF=3.
,﹣3),可得:BF=3.
连接MB交x轴于F.
∵CD⊥x轴,BM⊥x轴,∴CD∥BF.
∵C为A′B的中点,∴CD是△A′BF的中位线,得PE=CD=![]() BF=
BF=![]() .
.
∵点A的坐标是(2![]() ,0),∴当0<x<2
,0),∴当0<x<2![]() 时,点P应该在x轴的上方.
时,点P应该在x轴的上方.
可设点P的坐标为(x,![]() ),∴y=﹣x2+2
),∴y=﹣x2+2![]() x=
x=![]() ,解得:x=
,解得:x=![]() ±
±![]() ,满足0<x<2
,满足0<x<2![]() .
.
综上所述:存在点P(![]() +
+![]() )或(
)或(![]() ﹣
﹣![]() )使得四边形CDPE是平行四边形.
)使得四边形CDPE是平行四边形.

【题目】某校诗词知识竞赛培训活动中,在相同条件下对甲、乙两名学生进行了10次测验,他们的10次成绩如下(单位:分)

整理,分析过程如下:
成绩 学生 |
|
|
|
|
|
|
甲 | 0 | 1 | 4 | 5 | 0 | 0 |
乙 | 1 | 1 | 4 | 2 | 1 | 1 |
(1)两组数据的极差、平均数、中位数、众数、方差如下表所示,请补充完整:
学生 | 极差 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 83.7 | 86 | 13.21 | ||
乙 | 24 | 83.7 | 82 | 46.21 |
(2)若从甲、乙两人中选择一人参加知识竞赛,你会选 (填“甲”或“乙”),理由为 .