题目内容
【题目】平面内的两条直线有相交和平行两种位置关系

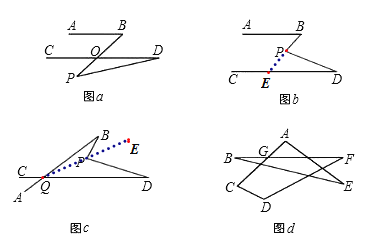
(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B﹣∠D.将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD、∠B、∠D、∠BQD之间有何数量关系?(不需证明)
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.
【答案】(1)不成立.结论是∠BPD=∠B+∠D,证明见解析;(2)![]() ;(3)360°.
;(3)360°.
【解析】
(1)延长BP交CD于E,根据两直线平行,内错角相等,求出∠PED=∠B,再利用三角形的一个外角等于和它不相邻的两个内角的和即可说明不成立,应为∠BPD=∠B+∠D;
(2)作射线QP,根据三角形的外角性质可得;
(3)根据四边形的内角和以及(2)的结论求解即可.
解:(1)不成立.结论是∠BPD=∠B+∠D
延长BP交CD于点E,
∵AB∥CD
∴∠B=∠BED
又∵∠BPD=∠BED+∠D,
∴∠BPD=∠B+∠D.
(2)结论:∠BPD=∠BQD+∠B+∠D.
作射线QP,
∵∠BPE是△BPQ的外角,∠DPE是△PDQ的外角,
∴∠BPE=∠B+∠BQE,∠DPE=∠D+∠DQP,
∴∠BPE+∠DPE=∠B+∠D+∠BQE+∠DQP,即∠BPD=∠BQD+∠B+∠D;
(3)在四边形CDFG中,∠CGF+∠C+∠D+∠F=360°,
又∵∠AGB=∠CGF,
∴∠AGB +∠C+∠D+∠F=360°,
由(2)知,∠AGB=∠B+∠A+∠E,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.

 中考解读考点精练系列答案
中考解读考点精练系列答案