题目内容
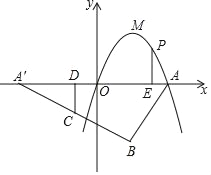
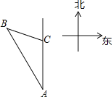
【题目】如图,某轮船沿正北方向航行,在点![]() 处测得灯塔
处测得灯塔![]() 在北偏西
在北偏西![]() 方向上,轮船以每小时
方向上,轮船以每小时![]() 海里的速度航行
海里的速度航行![]() 小时到达
小时到达![]() 后,测得灯塔
后,测得灯塔![]() 在北偏西
在北偏西![]() 方向上,问轮船到达灯塔
方向上,问轮船到达灯塔![]() 的正东方向时,轮船距灯塔有多远?(结果精确到
的正东方向时,轮船距灯塔有多远?(结果精确到![]() 海里,参考数据:
海里,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
【答案】此时轮船与灯塔![]() 之间的距离约为
之间的距离约为![]() 海里.
海里.
【解析】
首先作CD⊥AB于点D,作BE⊥AC于点E,进而得出△CDB为等腰直角三角形,再利用BE=![]() AB求出即可.
AB求出即可.
作CD⊥AB于点D,作BE⊥AC于点E,
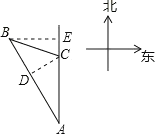
由题意可知,AC=50海里.
在Rt△ACD中,∵∠ADC=90°,∠A=30°,
∴CD=![]() AC=25海里,
AC=25海里,
AD=![]() CD=25
CD=25![]() 海里,
海里,
在Rt△BCD中,∵∠BDC=90°,∠CBD=75°30°=45°,
∴BD=CD=25海里,
∴AB=AD+BD=(25![]() +25)海里,
+25)海里,
Rt△ABE中,∵∠AEB=90°,∠A=30°,
∴BE=![]() AB=
AB=![]() ≈34.1(海里).
≈34.1(海里).
答:此时轮船与灯塔C之间的距离约为34.1海里.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目