题目内容
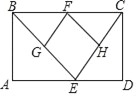
【题目】如图,在□ABCD 中,E、F为对角线AC上的两点,且AE=CF.

(1)求证:四边形DEBF是平行四边形;
(2)如果DE=3,EF=4,DF=5,求EB、DF两平行线之间的距离.
【答案】(1)详见解析;(2)2.4.
【解析】
(1)根据平行四边形的性质可得AD=BC,AD∥BC,继而可得∠DAE=∠BCF,然后即可利用SAS证明△ADF≌△CBE,进一步即可证明DF=EB,DF∥EB,即可证得结论;
(2)先根据勾股定理的逆定理得出DE⊥EF,然后根据三角形的面积即可求出结果.
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∴∠DAE=∠BCF,
∵AE=CF,∴AF=CE,
∴△ADF≌△CBE(SAS),
∴DF=EB,∠DFA=∠BEC,
∴DF∥EB,
∴四边形DEBF是平行四边形;
(2)解:∵![]() ,
,![]() ,
,
∴![]() ,∴DE⊥EF.
,∴DE⊥EF.
过点E作EG⊥DF于G,如图,则![]() ,即3×4=EG×5,∴EG=2.4.
,即3×4=EG×5,∴EG=2.4.
∴EB、DF两平行线之间的距离为2.4.


练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目