题目内容
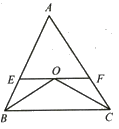
【题目】四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.
(1)利用图1,求证:四边形ABCD是菱形. 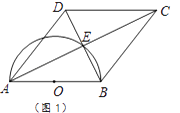
(2)如图2,若CD的延长线与半圆相切于点F,已知直径AB=8. ①连结OE,求△OBE的面积.
②求弧AE的长.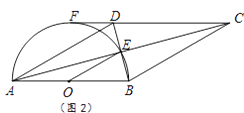
【答案】
(1)解:∵AE=EC,BE=ED,
∴四边形ABCD是平行四边形.
∵AB为直径,且过点E,
∴∠AEB=90°,即AC⊥BD.
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
(2)解:①连结OF.
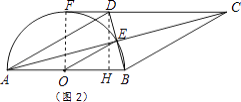
∵CD的延长线与半圆相切于点F,
∴OF⊥CF.
∵FC∥AB,
∴OF即为△ABD中AB边上的高.
∴S△ABD= ![]() AB×OF=
AB×OF= ![]() ×8×4=16,
×8×4=16,
∵点O是AB中点,点E是BD的中点,
∴S△OBE= ![]() S△ABD=4.
S△ABD=4.
②过点D作DH⊥AB于点H.
∵AB∥CD,OF⊥CF,
∴FO⊥AB,
∴∠F=∠FOB=∠DHO=90°.
∴四边形OHDF为矩形,即DH=OF=4.
∵在Rt△DAH中,sin∠DAB= ![]() =
= ![]() ,
,
∴∠DAH=30°.
∵点O,E分别为AB,BD中点,
∴OE∥AD,
∴∠EOB=∠DAH=30°.
∴∠AOE=180°﹣∠EOB=150°.
∴弧AE的长= ![]() =
= ![]() .
.
【解析】(1)先由AE=EC、BE=ED可判定四边形为平行四边形,再根据∠AEB=90°可判定该平行四边形为菱形;(2)①连结OF,由切线可得OF为△ABD的高且OF=4,从而可得S△ABD , 由OE为△ABD的中位线可得S△OBE= ![]() S△ABD; ②作DH⊥AB于点H,结合①可知四边形OHDF为矩形,即DH=OF=4,根据sin∠DAB=
S△ABD; ②作DH⊥AB于点H,结合①可知四边形OHDF为矩形,即DH=OF=4,根据sin∠DAB= ![]() =
= ![]() 知∠EOB=∠DAH=30°,即∠AOE=150°,根据弧长公式可得答案
知∠EOB=∠DAH=30°,即∠AOE=150°,根据弧长公式可得答案

【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.