��Ŀ����
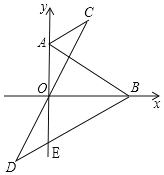
����Ŀ����֪OΪֱ��AB�ϵ�һ��,��COE��ֱ��,OFƽ�֡�AOE(ͼ����˵�ĽǶ���С��ƽ�ǵĽ�).
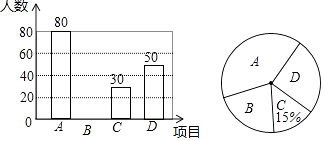
(1)��ͼ1,����COF=28��,���BOE=______�㣻����COF=![]() ���BOE=_______����BOE���COF��������ϵΪ_________��
���BOE=_______����BOE���COF��������ϵΪ_________��
(2)����COE�Ƶ�O��ʱ����ת����ͼ2��ʾ��λ��ʱ,(1)�С�BOE�͡�COF��������ϵ����Ȼ����������������˵�����ɣ����������������BOE���COF��������ϵ��
(3)����COE�Ƶ�O˳ʱ����ת����ͼ3��λ��ʱ,(1)�С�BOE�͡�COF��������ϵ�Ƿ���Ȼ����?����������˵�����ɣ���������,�������BOE���COF��������ϵ.
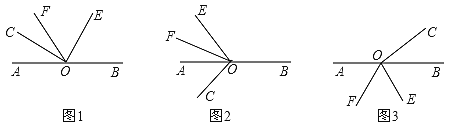
���𰸡�(1) 56�㣻2m�㣻��BOE=2��COF����2�����������������������3����BOE�͡�COF�Ĺ�ϵ����������BOE�͡�COF�Ĺ�ϵΪ��BOE��2��EOF��360�㣬�����������.
��������
��1����֪��COF=28�㣬��COE��ֱ�ǣ��ɴ���á�EOF=62�㣬����OFƽ�֡�AOE�����ݽ�ƽ���ߵĶ���ɵá�AOE=2��EOF=124�㣬����ƽ�ǵĶ��弴����á�BOE=56�㣻�ɡ�COF=m�㣬��COE��ֱ�ǣ��ɵá�EOF=90��-m�㣬��֪OFƽ�֡�AOE���ɽ�ƽ���ߵĶ���ɵá�AOE=2��EOF=2��90��-m�㣩��������á�BOE=2m�㣬�ɴ˿ɵá�BOE=2��COF����2����������ȣ�1���ķ�����ɣ���3������������֪��COE��ֱ�ǣ��ɵá�EOF����COF��90�㣬��֪OFƽ�֡�AOE���ɽ�ƽ���ߵĿɵá�AOE��2��EOF������ƽ�ǵĶ���ɵá�BOE��180�㣭��AOE��180�㣭2(��COF��90��)��360�㣭2��COF���ɴ˿ɵá�BOE��2��EOF��360��.
��1���ߡ�COF=28�㣬��COE��ֱ�ǣ�
���EOF=90��-28��=62�㣬
�֡�OFƽ�֡�AOE��
���AOE=2��EOF=124�㣬
���BOE=180��-124��=56�㣬
�ߡ�COF=m�㣬��COE��ֱ�ǣ�
���EOF=90��-m�㣬
�֡�OFƽ�֡�AOE��
���AOE=2��EOF=2��90��-m�㣩��
���BOE=180��-2��90��-m�㣩=2m�㣬
���BOE=2��COF.
�ʴ���56�㣻2m�㣻��BOE=2��COF��
��2����BOE�͡�COF�Ĺ�ϵ��Ȼ������
�ߡ�COE��ֱ�ǣ�
���EOF=90��-��COF��
�֡�OFƽ�֡�AOE��
���AOE=2��EOF��
���BOE=180��-��AOE=180��-2��90��-��COF��=2��COF��
��3����BOE�͡�COF�Ĺ�ϵ���������������£�
�ߡ�COE��ֱ�ǣ�
���EOF����COF��90�㣬
�֡�OFƽ�֡�AOE��
���AOE��2��EOF��
���BOE��180�㣭��AOE��180�㣭2(��COF��90��)��360�㣭2��COF��
���BOE��2��EOF��360��.

����Ŀ��ij��ѧ���꼶![]() ����ѧ������ȤС����̽������
����ѧ������ȤС����̽������![]() ���ι��ж������Խ��ߡ���һ����ʱ����������±���
���ι��ж������Խ��ߡ���һ����ʱ����������±���
����εı��� |
|
|
|
|
| �� |
�Ӷ����һ���������������ĶԽ������� | �� | |||||
����ζԽ��ߵ������� | �� |
![]() ̽�����������Ǹ�С��ij�Ա��������о��Ľ�������ϱ���
̽�����������Ǹ�С��ij�Ա��������о��Ľ�������ϱ���
![]() ���룺���ű��������ӣ�����ζԽ��ߵ�������Խ��Խ�࣬��
���룺���ű��������ӣ�����ζԽ��ߵ�������Խ��Խ�࣬��![]() ���ε�һ��������������ĶԽ�������Ϊ���٣�
���ε�һ��������������ĶԽ�������Ϊ���٣�![]() ���ζԽ��ߵ�������Ϊ���٣�
���ζԽ��ߵ�������Ϊ���٣�
![]() Ӧ�ã�
Ӧ�ã�![]() ���˾ۻᣬÿ�����ڵ��˶���һ���֣����ն��ٴ��֣�
���˾ۻᣬÿ�����ڵ��˶���һ���֣����ն��ٴ��֣�