题目内容
【题目】函数y=x2+bx+c与y=x的图象如图所示，有以下结论： ①b2﹣4c＞0；
②b+c+1=0；
③3b+c+6=0；
④当1＜x＜3时，x2+（b﹣1）x+c＜0．
其中正确的个数为（ ）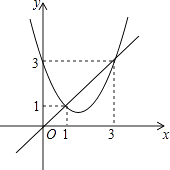
A.1个
B.2个
C.3个
D.4个
【答案】B
【解析】解：∵函数y=x2+bx+c与x轴无交点， ∴b2﹣4ac＜0；
故①错误；
当x=1时，y=1+b+c=1，
故②错误；
∵当x=3时，y=9+3b+c=3，
∴3b+c+6=0；
③正确；
∵当1＜x＜3时，二次函数值小于一次函数值，
∴x2+bx+c＜x，
∴x2+（b﹣1）x+c＜0．
故④正确．
故选B
由函数y=x2+bx+c与x轴无交点，可得b2﹣4c＜0；当x=1时，y=1+b+c=1；当x=3时，y=9+3b+c=3；当1＜x＜3时，二次函数值小于一次函数值，可得x2+bx+c＜x，继而可求得答案．
练习册系列答案
相关题目
【题目】某中学八年级
班数学课外兴趣小组在探究：“
边形共有多少条对角线”这一问题时，设计了如下表格：
多边形的边数 |
|
|
|
|
| … |
从多边形一个顶点出发可引起的对角线条数 | … | |||||
多边形对角线的总条数 | … |
探究：假若你是该小组的成员，请把你研究的结果填入上表；
猜想：随着边数的增加，多边形对角线的条数会越来越多，从边形的一个顶点出发可引的对角线条数为多少，边形对角线的总条数为多少．
应用：
个人聚会，每不相邻的人都握一次手，共握多少次手？
