题目内容
在直角坐标平面中,O为坐标原点,二次函数y=-x2-2x+3的图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,点D、C关于抛物线的对称轴对称.
(1)求四边形ABCD的面积;
(2)在y轴上找一点P,使△ABP是直角三角形,并求出点P的坐标.
(1)求四边形ABCD的面积;
(2)在y轴上找一点P,使△ABP是直角三角形,并求出点P的坐标.
(1)设y=0,则y=-x2-2x+3=0,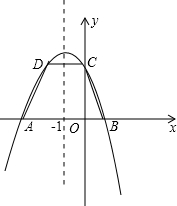
解得:x=-3或1,
∵点A在点B的左侧,
∴A(-3,0),B(1,0),
设x=0,则y=3,
∴C(0,3),
∵抛物线的对称轴为x=-
=-1,
∴D(-2,3),
∵点D、C关于抛物线的对称轴对称,
∴四边形ABCD为梯形,
∴SABCD=
=
=6;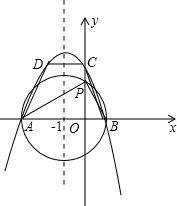
(2)如图所示:依AB为直径画圆,交y轴于点P,
∵AB为圆的直径,
∴∠APB=90°,
∴三角形APC是直角三角形,
∵OP⊥AB,
∴OP2=AO•BO=3×1=3,
∴OP=
,
∴点P(0,
)或(0,-
).

解得:x=-3或1,
∵点A在点B的左侧,
∴A(-3,0),B(1,0),
设x=0,则y=3,
∴C(0,3),
∵抛物线的对称轴为x=-
| b |
| 2a |
∴D(-2,3),
∵点D、C关于抛物线的对称轴对称,
∴四边形ABCD为梯形,
∴SABCD=
| (AB+DC)×OC |
| 2 |
| 4×3 |
| 2 |

(2)如图所示:依AB为直径画圆,交y轴于点P,
∵AB为圆的直径,
∴∠APB=90°,
∴三角形APC是直角三角形,
∵OP⊥AB,
∴OP2=AO•BO=3×1=3,
∴OP=
| 3 |
∴点P(0,
| 3 |
| 3 |

练习册系列答案
相关题目


