题目内容
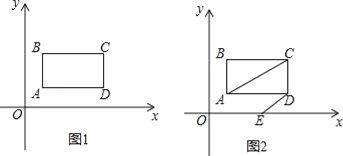
【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系式![]() .
.
(1)求a,b,c的值;
(2)如果在第二象限内有一点P(m,![]() ),使四边形ABOP的面积与三角形ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
),使四边形ABOP的面积与三角形ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(1)a=2,b=3,c=4;(2)P(-3,![]() ).
).
【解析】
(1)用非负数的性质求解可得a,b,c的值;
(2)把四边形ABOP的面积看成两个三角形面积和,用m来表示;依据四边形ABOP的面积与三角形ABC的面积相等,列方程即可.
(1)由已知![]() ,
,
可得:a-2=0,b-3=0,c-4=0,
解得a=2,b=3,c=4;
(2)∵S△ABO=![]() ×2×3=3,S△APO=
×2×3=3,S△APO=![]() ×2×(-m)=-m,
×2×(-m)=-m,
∴S四边形ABOP=S△ABO+S△APO=3+(-m)=3-m;
∵S△ABC=![]() ×4×3=6,
×4×3=6,
又∵S四边形ABOP=S△ABC
∴3-m=6,
解得m=-3,
∴存在点P(-3,![]() )使S四边形ABOP=S△ABC.
)使S四边形ABOP=S△ABC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目