题目内容
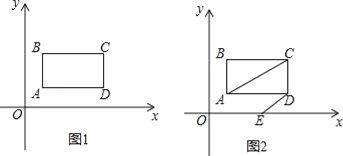
【题目】如图1，在平面直角坐标系中，第一象限内长方形ABCD，AB∥y轴，点A（1，1），点C（a，b），满足
+|b﹣3|=0．
（1）求长方形ABCD的面积．
（2）如图2，长方形ABCD以每秒1个单位长度的速度向右平移，同时点E从原点O出发沿x轴以每秒2个单位长度的速度向右运动，设运动时间为t秒．
①当t=4时，直接写出三角形OAC的面积为 ；
②若AC∥ED，求t的值；
（3）在平面直角坐标系中，对于点P（x，y），我们把点P′（﹣y+1，x+1）叫做点P的伴随点，已知点A1的伴随点为A2，点A2的伴随点为A3，点A3的伴随点为A4，…，这样依次得到点A1，A2，A3，…，An．
①若点A1的坐标为（3，1），则点A3的坐标为 ，点A2014的坐标为 ；
②若点A1的坐标为（a，b），对于任意的正整数n，点An均在x轴上方，则a，b应满足的条件为 ．
【答案】（1）8;
（2）①3．
②当AC∥ED，t的值为3秒．
（3）①（﹣3，1）；（0，4）．
②﹣1＜a＜1，0＜b＜2．
【解析】试题分析：(1)、首先根据非负数的形状得出a和b的值，然后根据长方形的形状得出点B、点C和点D的坐标，从而得出长方形的面积；(2)、将t=4时的图像画出来，然后根据三角形的面积计算法则得出答案；过点D做DF垂直x轴于F点，根据平行线的形状得出∠CAD=∠DEF，当运动时间为t时，点D（5+t，1），点F（5+t，0），E（2t，0），从而得出答案；(3)、首先根据题意先写出前面的几个点的坐标，从而得出点的坐标循环规律，从而得出所要求的点坐标；首先根据题意先写出前面的几个点的坐标，根据点所在的位置列出不等式组，从而得出a和b的取值范围．
试题解析：(1)、∵
+|b﹣3|=0， ∴a﹣5=0，b﹣3=0，即a=5，b=3，
∵四边形ABCD为长方形， ∴点B（1，3），点C（5，3），点D（5，1），
∴AB=3﹣1=2，BC=5﹣1=4， 长方形ABCD的面积为AB×BC=2×4=8．
(2)、①将t=4时，线段AC拿出来，放在图3中，各字母如图，
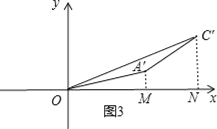
∵点A′（5，1），点C′（9，3）， ∴OM=5，ON=9，A′M=1，C′N=3，MN=ON﹣OM=4，
三角形OA′C′的面积=
ONC′N﹣OMA′M﹣
（A′M+C′N）MN=
﹣
﹣
=
=3；
②过点D做DF垂直x轴于F点，如图2，
∵AC∥ED， ∴∠CAD=∠ADE（两直线平行，内错角相等），
∵AD∥x轴， ∴∠DEF=∠ADE（两直线平行，内错角相等）， ∴∠CAD=∠DEF，
当运动时间为t时，点D（5+t，1），点F（5+t，0），E（2t，0），
则
=
，解得t=3秒， 故当AC∥ED，t的值为3秒；
(3)、①根据题意可知：A1（3，1），A2（0，4），A3（﹣3，1），A4（0，﹣2），A5（3，1），
由此发现此组数据以4个为一组进行循环，
2014÷4=503…2，即A2014=A2，
故答案为：（﹣3，1）；（0，4）．
②根据题意可知：A1（a，b），A2（1﹣b，a+1），A3（﹣a，2﹣b），A4（b﹣1，1﹣a），A5（a，b），
由此发现此组数据以4个为一组进行循环，
∵对于任意的正整数n，点An均在x轴上方，则有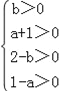
，
解得﹣1＜a＜1，0＜b＜2．
