题目内容
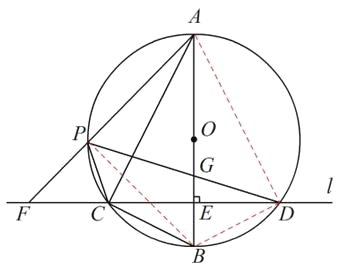
【题目】如图，在⊙O的内接三角形ABC中，∠ACB＝90°，AC＝2BC，过C作AB的垂线l交⊙O于另一点D，垂足为E.设P是
上异于A，C的一个动点，射线AP交l于点F，连接PC与PD，PD交AB于点G.
(1)求证：△PAC∽△PDF；
(2)若AB＝5，
，求PD的长；
(3)在点P运动过程中，设
＝x，tan∠AFD＝y，求y与x之间的函数关系式．(不要求写出x的取值范围)
【答案】（1）证明见解析；（2）
；（3）
.
【解析】试题分析：（1）应用圆周角定理证明∠APD＝∠FPC，得到∠APC＝∠FPD，又由∠PAC＝∠PDC，即可证明结论.
（2）由AC=2BC，设
，应用勾股定理即可求得BC，AC的长，则由AC=2BC得
，由△ACE∽△ABC可求得AE，CE的长，由
可知△APB是等腰直角三角形，从而可求得PA的长，由△AEF是等腰直角三角形求得EF=AE=4，从而求得DF的长，由（1）△PAC∽△PDF得
，即可求得PD的长.
（3）连接BP，BD，AD，根据圆的对称性，可得
，由角的转换可得
，由△AGP∽△DGB可得
，由△AGD∽△PGB可得
，两式相乘可得结果.
试题解析：（1）由APCB内接于圆O，得∠FPC＝∠B，
又∵∠B＝∠ACE＝90°－∠BCE，∠ACE＝∠APD，∴∠APD＝∠FPC.
∴∠APD＋∠DPC＝∠FPC＋∠DPC，即∠APC＝∠FPD.
又∵∠PAC＝∠PDC，∴△PAC∽△PDF.
（2）连接BP，设，∵∠ACB=90°，AB=5，∴
.∴
.
∵△ACE∽△ABC，∴
，即
. ∴
.
∵AB⊥CD，∴
.
如图，连接BP，
∵，∴△APB是等腰直角三角形. ∴∠PAB＝45°，
.
∴△AEF是等腰直角三角形. ∴EF=AE=4. ∴DF=6.
由（1）△PAC∽△PDF得，即
.
∴PD的长为.
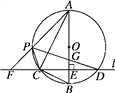
（3）如图，连接BP，BD，AD，
∵AC=2BC，∴根据圆的对称性，得AD=2DB，即.
∵AB⊥CD，BP⊥AE，∴∠ABP＝∠AFD.
∵
，∴.
∵△AGP∽△DGB，∴.
∵△AGD∽△PGB，∴.
∴
，即
.
∵
，∴
.
∴
与
之间的函数关系式为.
