Question

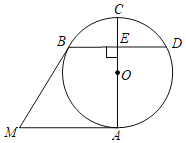
【题目】如图，⊙O中，AC为直径，MA，MB分别切⊙O于点A，B，过点B作BD⊥AC于点E，交⊙O于点D，若BD＝MA，则∠AMB的大小为_____度．

Answer 1

【答案】60．

【解析】

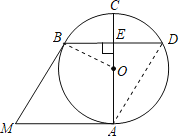
连接AD、OB，根据切线的性质定理得到OB⊥MB，OA⊥MA，根据菱形的性质得到∠AMB＝∠D，根据圆周角定理得到∠AOB＝2∠D，计算即可．

解：连接AD、OB，

∵MA，MB分别切⊙O于点A，B，

∴OB⊥MB，OA⊥MA，MA＝MB，

∵OA⊥MA，BD⊥AC，

∴BD∥MA，又BD＝MA，

∴四边形BMAD为平行四边形，

∵MA＝MB，

∴四边形BMAD为菱形，

∴∠AMB＝∠D，

由圆周角定理得，∠AOB＝2∠D，

∵OB⊥MB，OA⊥MA，

∴∠AMB+∠AOB＝180°，

∴∠AMB+2∠D＝180°，

∴∠AMB＝60°，

故答案为：60．