��Ŀ����
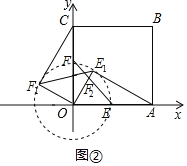
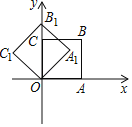
����Ŀ����֪������OABC��ƽ��ֱ������ϵ�У���A��C�ֱ���x�ᣬy����������ϣ�����ֱ��������OEF��ֱ�Ƕ���O��ԭ�㣬E��F�ֱ���OA��OC�ϣ���OA��4��OE��2������OEF�Ƶ�O��ʱ����ת���á�OE1F1����E��F��ת��Ķ�Ӧ��ΪE1��F1��
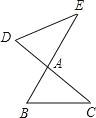
������ͼ�٣���E1F1�ij�������ͼ�ڣ�����CF1��AE1����֤��OAE1�ա�OCF1��
������OEF�Ƶ�O��ʱ����תһ�ܣ���OE1��CF1ʱ�����E1�����ֱ꣨��д��������ɣ���

���𰸡�����2![]() ����֤��������������1��
����֤��������������1��![]() ����1����
����1����![]() ����
����
��������
�����ɵ���ֱ�������ε����ʺ��ɶ������EF��������ת�����ʼ��ɵó��𰸣��ڸ�����ת�������ҵ���ȵ��߶Σ�����SAS����֤����
�������ڡ�OEF�ǵ���Rt������OE��CF����ôCF����OF��ֱ������ת�����У�E��F�Ĺ켣����OΪԲ�ģ�OE����OF����Ϊ�뾶��Բ����CF��OF����ôCF��Ϊ��O�����ߣ����е�ΪF���ɹ�C����O�����ߣ���ô�������е㶼����F���Ҫ����˶�Ӧ��E��Ҳ����������Rt��OFC�У�OF��2��OC��OA��4����֤�á�FCO��30��������EOC��30������֪��OE�ij���ͨ����ֱ�������Σ��õ�E������꣬�ɴ˵ý⣮
���ٽ⣺�ߵ���ֱ��������OEF��ֱ�Ƕ���O��ԭ�㣬OE��2��
���EOF��90����OF��OE��2��
��EF��![]() ��
��![]() ��2
��2![]() ��
��
�߽���OEF�Ƶ�O��ʱ����ת���á�OE1F1��
��E1F1��EF��2![]() ��
��
��֤�������ı���OABCΪ�����Σ�
��OC��OA��
�߽���OEF�Ƶ�O��ʱ����ת���á�OE1F1��
���AOE1����COF1��
�ߡ�OEF�ǵ���ֱ�������Σ�
���OE1F1�ǵ���ֱ�������Σ�
��OE1��OF1��
�ڡ�OAE1�͡�OCF1�У�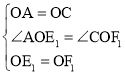
���OAE1�ա�OCF1��SAS����
���⣺��OE��OF��
�����F��OEƽ�е�ֱ������ֻ��һ��������OF��ֱ��
�����ǰ�OEF��O����ʱ����תһ��ʱ��
���F����OΪԲ�ģ���OFΪ�뾶��Բ�ϣ�
�����F��OF��ֱ��ֱ�߱���ԲO�����ߣ�
�ֵ�C��ԲO��һ�㣬����C��ԲO���е�ֱ������ֻ��2����������ΪCF1��CF2��
��ʱ��E��ֱ���E1���E2�㣬����CF1��OE1��CF2��OE2��
���е�F1�ڵڶ�����ʱ����E1�ڵ�һ���ޣ�
��ֱ��������CF1O�У�OC��4��OF1��2��
cos��COF1��![]() ��
��![]() ��
��![]() ��
��
���COF1��60����
���AOE1��60����
���E1�ĺ����ꣽ2cos60����1��
��E1�������ꣽ2sin60����![]() ��
��
���E1��������1��![]() ����
����
���е�F2�ڵ�һ����ʱ����E2�ڵ������ޣ�
ͬ������E2������Ϊ��1����![]() ����
����
������������OE1��CF1ʱ����E1������Ϊ��1��![]() ����1����
����1����![]() ����
����