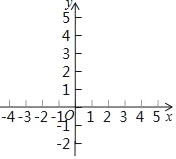题目内容
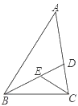
【题目】已知△ABC与△DEC是两个大小不同的等腰直角三角形.
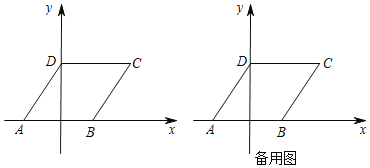
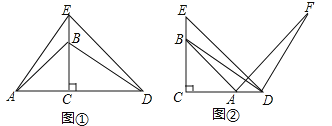
(1)如图①所示,连接AE,DB,试判断线段AE和DB的数量和位置关系,并说明理由;
(2)如图②所示,连接DB,将线段DB绕D点顺时针旋转90°到DF,连接AF,试判断线段DE和AF的数量和位置关系,并说明理由.
【答案】(1)AE=DB,AE⊥DB;(2)DE=AF,DE⊥AF.
【解析】试题分析:(1)根据等腰直角三角形的性质、全等三角形的判定定理证明Rt△BCD≌Rt△ACE,根据全等三角形的性质解答;
(2)证明△EBD≌△ADF,根据全等三角形的性质证明即可.
试题解析:解:(1)AE=DB,AE⊥DB.证明如下:
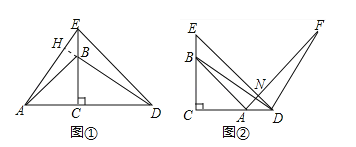
∵△ABC与△DEC是等腰直角三角形,∴AC=BC,EC=DC,在Rt△BCD和Rt△ACE中,∵AC=BC,∠ACE=∠BCD,CE=CD,∴Rt△BCD≌Rt△ACE,∴AE=BD,∠AEC=∠BDC,∵∠BCD=90°,∴∠DHE=90°,∴AE⊥DB;
(2)DE=AF,DE⊥AF.证明如下:
设DE与AF交于N,由题意得,BE=AD,∵∠EBD=∠C+∠BDC=90°+∠BDC,∠ADF=∠BDF+∠BDC=90°+∠BDC,∴∠EBD=∠ADF,在△EBD和△ADF中,∵BE=AD,∠EBD=∠ADF,DE=DF,∴△EBD≌△ADF,∴DE=AF,∠E=∠FAD,∵∠E=45°,∠EDC=45°,∴∠FAD=45°,∴∠AND=90°,即DE⊥AF.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案【题目】问题:探究函数的图象与性质.小华根据学习函数的经验,对函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:在函数y=|x|﹣2中,自变量x可以是任意实数;
Ⅰ如表是y与x的几组对应值.
y | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
x | … | 1 | 0 | ﹣1 | ﹣2 | ﹣1 | 0 | m | … |
①m= ;
②若A(n,8),B(10,8)为该函数图象上不同的两点,则n= ;
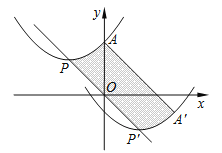
Ⅱ如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;根据函数图象可得:
①该函数的最小值为 ;
②该函数的另一条性质是 .