Question

【题目】如图，点P是⊙O外一点，PA切⊙O于点A，AB是⊙O的直径，连接OP，过点B作BC∥OP交⊙O于点C，连接AC交OP于点D．

（1）求证：PC是⊙O的切线；

（2）若PD=cm，AC=8cm，求图中阴影部分的面积；

（3）在（2）的条件下，若点E是弧AB的中点，连接CE，求CE的长．

Answer 1

【答案】（1）证明见解析；

（2）阴影部分的面积为；

（3）CE的长是

【解析】（1）连接OC，证明△PAO≌△PCO，得到∠PAO=∠PCO=90 ，证明结论；

（2）证明△ADO∽△PDA，得到成比例线段求出BC的长，根据S阴=S半⊙O－S△ACB求出答案；

（3）连接AE，BE，过点B作BM⊥CE于点M，分别求出CM和EM的长，求和得到答案．

证明： ⑴如图，连接OC，

∵PA切⊙O于A．

∴∠PAO=90．

∵OP∥BC，

∴∠AOP=∠OBC，∠COP=∠OCB．

∵OC=OB，

∴∠OBC=∠OCB，

∴∠AOP=∠COP．

又∵OA=OC，OP=OP，

∴△PAO≌△PCO (SAS)．

∴∠PAO=∠PCO=90 ，

又∵OC是⊙O的半径，

∴PC是⊙O的切线．

⑵解法一：

由（1）得PA，PC都为圆的切线，

∴PA=PC，OP平分∠APC，∠ADO=∠PAO=90 ，

∴∠PAD+∠DAO=∠DAO+∠AOD，

∴∠PAD =∠AOD，

∴△ADO∽△PDA．

∴，

∴，

∵AC=8， PD=，

∴AD=AC=4，OD=3，AO=5，

由题意知OD为△ABC的中位线，

∴BC=2OD=6，AB=10．

∴S阴=S半⊙O－S△ACB=．

答：阴影部分的面积为．

解法二：

∵AB是⊙O的直径，OP∥BC，

∴∠PDC=∠ACB=90．

∵∠PCO=90 ，

∴∠PCD+∠ACO=∠ACO+∠OCB=90 ，

即∠PCD=∠OCB．

又∵∠OBC =∠OCB，

∴∠PCD=∠OBC，

∴△PDC∽△ACB，

∴．

又∵AC=8， PD=，

∴AD=DC=4，PC=．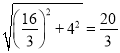

∴，

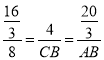∴CB=6，AB=10，

∴S阴=S半⊙O-S△ACB=．

答：阴影部分的面积为．

（3）如图，连接AE，BE，过点B作BM⊥CE于点M．

∴∠CMB=∠EMB=∠AEB=90，

又∵点E是的中点，

∴∠ECB=∠CBM=∠ABE=45，CM=MB =，BE=ABcos45=，

∴ EM=，

∴CE=CM+EM=．

“点睛”本题考查的是切线的判定和性质、扇形面积的计算和相似三角形的判定和性质，灵活运用切线的性质：圆的切线垂直于过切点的半径和切线的判定是解题的关键．