题目内容
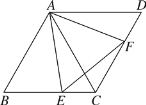
【题目】如图,△ABC和△ACD均为等边三角形,E是BC上的一个动点,F是CD上的一个动点,且∠EAF=60°.
(1)请判断△AEF的形状,并说明理由;
(2)当AB=4时,求△AEF面积的最小值.
【答案】(1)见解析;(2)3![]() .
.
【解析】(1)由等边三角形的性质得到AD=AC,∠D=∠ACB=60°,∠BAC=∠CAD=60°.再由∠EAF=60°,得到∠EAC=∠FAD.即可证明△AEC≌△AFD,由全等三角形的性质得到AE=AF,即可得到△AEF是等边三角形.
(2)由△AEF为等边三角形,得到S△AEF=![]() AE2.要使S△AEF最小,则需使AE最小,当AE⊥BC时,AE最小.求出AE的最小值,代入计算即可.
AE2.要使S△AEF最小,则需使AE最小,当AE⊥BC时,AE最小.求出AE的最小值,代入计算即可.
(1)△AEF是等边三角形.理由如下:
∵△ABC和△ACD均为等边三角形,∴AD=AC,∠D=∠ACB=60°,∠BAC=∠CAD=60°.
又∵∠EAF=60°,∴∠EAC=∠FAD.在△AEC与△AFD中,∵∠EAC=∠FAD,AC=AD,∠ACE=∠D,∴△AEC≌△AFD(ASA),∴AE=AF.
又∵∠EAF=60°,∴△AEF是等边三角形.
(2)由(1)知△AEF为等边三角形,∴S△AEF=![]() AE2.要使S△AEF最小,则需使AE最小,当AE⊥BC时,AE最小.此时.在Rt△ABE中,∵AB=4,∠B=60°,∴∠BAE=30°,∴BE=
AE2.要使S△AEF最小,则需使AE最小,当AE⊥BC时,AE最小.此时.在Rt△ABE中,∵AB=4,∠B=60°,∴∠BAE=30°,∴BE=![]() AB=2,∴AE=
AB=2,∴AE=![]() .∴S△AEF的最小值为
.∴S△AEF的最小值为![]() ×(
×(![]() )2=
)2=![]() .
.

【题目】如图,某计算装置有一數据输入口A和一运算结果的输出口B,表格中是小明输入的一些数据和这些数据经该装置计算后输出的相应结果,按照这个计算装置的计算规律,若输入的数是10,则输出的数是( )
A | 1 | 2 | 3 | 4 | 5 |
B | 0 | 3 | 8 | 15 | 24 |
A. 99 B. 100 C. 101 D. 102