题目内容
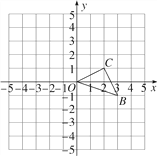
【题目】如图,已知O是坐标原点,B,C两点的坐标分别为(3,-1),(2,1).
(1)以O点为位似中心,在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
(2)如果△OBC内部一点M的坐标为(x,y),写出B,C,M的对应点B′,C′,M′的坐标.
【答案】(1)如图所示见解析;(2)B′(-6,2),C′(-4,-2),M′(-2x,-2y).
【解析】分析:(1)根据位似图形的性质:以某点为位似中心的两个图形的对应点到位似中心的距离之比等于位似比,且对应点的连线与位似中心在同一直线上,根据位似图形的性质和已知图形的各顶点和位似比,求出位似后的对应点,然后再连接各点.
(2)根据位似图形的性质即可求解.
详解:(1)如图所示,
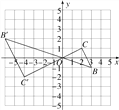
(2)如图所示:∵B,C两点的坐标分别为(3,-1),(2,1),新图与原图的相似比为2,
∴B′(-6,2),C′(-4,-2),
∵△OBC内部一点M的坐标为(x,y),
∴对应点M′(-2x,-2y).

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目