题目内容
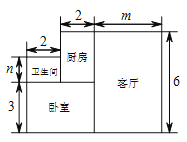
【题目】如图所示是长方体纸盒的平面展开图,设 AB=x cm,若 AD =4x cm,AN=3x cm.
(1)求长方形 DEFG 的周长与长方形 ABMN 的周长(用字母 x 进行表示);
(2)若长方形 DEFG 的周长比长方形 ABMN 的周长少 8cm,求 x 的值;
(3)在第(2)问的条件下,求原长方体纸盒的容积.

【答案】(1)6x,8x;(2)x=4;(3)384.
【解析】
(1)根据AB=x,若AD=4x,AN=3x,即可得到长方形DEFG的周长与长方形ABMN的周长;
(2)根据长方形DEFG的周长比长方形ABMN的周长少8,得到方程,即可得到x的值;
(3)根据原长方体的容积为x2x3x=6x3,代入x的值即可得到原长方体的容积.
(1)∵AB=x,若AD=4x,AN=3x,
∴长方形DEFG的周长为2(x+2x)=6x,
长方形ABMN的周长为2(x+3x)=8x;
(2)依题意,8x-6x=8,
解得:x=4;
(3)原长方体的容积为x2x3x=6x3,
将x=4代入,可得容积6x3=384.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目