��Ŀ����
����Ŀ����ͼ���ڱ߳�Ϊ4��������ABCD�У�P��BC����һ���㣨����B��C���㣩������ABP��ֱ��AP���ۣ���B���ڵ�E������CD����һ��M��ʹ�ý���CMP��ֱ��MP���ۺ�C����ֱ��PE�ϵĵ�F����ֱ��PE��CD�ڵ�N������MA��NA�������½�������ȷ������д��������ȷ���۵���ţ�
�١�CMP�ס�BPA��
���ı���AMCB��������ֵΪ10��
�۵�PΪBC�е�ʱ��AEΪ�߶�NP���д��ߣ�
���߶�AM����СֵΪ2 ![]() ��
��
�ݵ���ABP�ա�ADNʱ��BP=4 ![]() ��4��
��4��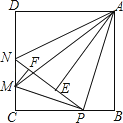
���𰸡��٢ڢ�
���������⣺�ߡ�APB=��APE����MPC=��MPN��
�ߡ�CPN+��NPB=180�㣬
��2��NPM+2��APE=180�㣬
���MPN+��APE=90�㣬
���APM=90�㣬
�ߡ�CPM+��APB=90�㣬��APB+��PAB=90�㣬
���CPM=��PAB��
���ı���ABCD�������Σ�
��AB=CB=DC=AD=4����C=��B=90�㣬
���CMP�ס�BPA���ʢ���ȷ��
��PB=x����CP=4��x��
�ߡ�CMP�ס�BPA��
�� ![]() =
= ![]() ����CM=
����CM= ![]() x��4��x������S�ı���AMCB=
x��4��x������S�ı���AMCB= ![]() [4+
[4+ ![]() x��4��x��]��4=��
x��4��x��]��4=�� ![]() x2+2x+8=��
x2+2x+8=�� ![]() ��x��2��2+10��
��x��2��2+10��
��x=2ʱ���ı���AMCB������ֵΪ10���ʢ���ȷ��
��PB=PC=PE=2ʱ����ND=NE=y��
��RT��PCN����y+2��2=��4��y��2+22���y= ![]() ��
��
��NE��EP���ʢ۴���
��MG��AB��G��
��AM= ![]() =
= ![]() ��
��
��AG��СʱAM��С��
��AG=AB��BG=AB��CM=4�� ![]() x��4��x��=
x��4��x��= ![]() ��x��1��2+3��
��x��1��2+3��
��x=1ʱ��AG��Сֵ=3��
��AM����Сֵ= ![]() =5���ʢܴ���
=5���ʢܴ���
�ߡ�ABP�ա�ADNʱ��
���PAB=��DAN=22.5�㣬��AB��ȡһ��Kʹ��AK=PK����PB=z��
���KPA=��KAP=22.5��
�ߡ�PKB=��KPA+��KAP=45�㣬
���BPK=��BKP=45�㣬
��PB=BK=z��AK=PK= ![]() z����z+
z����z+ ![]() z=4����z=4
z=4����z=4 ![]() ��4����PB=4
��4����PB=4 ![]() ��4�ʢ���ȷ��
��4�ʢ���ȷ��
�ʴ�Ϊ�٢ڢݣ�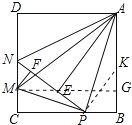
����ȷ��ֻҪ֤����APM=90�㼴�ɽ�����⣮
����ȷ����PB=x���������κ��������ö��κ������ʽ�����⼴�ɣ�
�۴�����ND=NE=y����RT��PCN�У����ù��ɶ������y���ɽ�����⣮
�ܴ�����MG��AB��G����ΪAM= ![]() =
= ![]() ������AG��СʱAM��С���������κ��������AG����СֵΪ3��AM����СֵΪ5��
������AG��СʱAM��С���������κ��������AG����СֵΪ3��AM����СֵΪ5��
����ȷ����AB��ȡһ��Kʹ��AK=PK����PB=z���г����̼��ɽ�����⣮���⿼���������ۺ��⡢�����ε����ʡ����������ε��ж������ʡ�ȫ�������ε����ʡ����ɶ�����֪ʶ������Ĺؼ���ѧ�ṹ�����κ��������ֵ���⣬ѧ�����ӳ��ø����ߣ������п�ѹ���⣮

 �������ϵ�д�
�������ϵ�д�����Ŀ��ij���ز������� 2010 �� 6 �´����д��� 3 ��Ԫ����ij¥�̣����� ����Ϊ���꣬����������Ϊ 8%����¥���� A��B ���ֻ����� 500 ������ �����سɱ��������ɱ������۳ɱ���A ���ͷ�ƽ��ÿƽ���׳ɱ�Ϊ 0.6 ��Ԫ��
B ���ͷ�ƽ��ÿƽ���׳ɱ�Ϊ 0.7 ��Ԫ�����ǿ�����ԭ�������ر���
���������m2�� | ���ۼ۸���Ԫ/m2�� | |
A ���� | 75 | 0.8 |
B ���� | 100 | 1 |
��1����¥�����ֻ��ͷ����ж����ף�
��2�����������ߵ�ʵʩ��2011 ���������ز��г�ή�Ҳ��������ּ����������������֮ǰ�ѷ����꣬2012 �� 1 ��ʵ�ʿ���ʱ�� A ���ͷ���ԭ���� �ۼ۴� 9 �ۣ�B ���ͷ���ԭ�����ۼ۴� 8.3 �۳��ۣ���� 2012 �� 6 ��ǰ���� �ֻ��͵ķ�ȫ�����꣬�������ڻ�����������Ϣ֮������������Ԫ�� ʵ�����۶��ԭ�����۶��½��˰ٷ�֮����