题目内容
【题目】在矩形ABCD中,∠ABC的平分线交边AD于点E,∠BED的平分线交直线CD于点F.若AB=3,CF=1,则BC=_____.
【答案】2![]() +1或
+1或![]()
【解析】
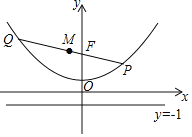
如图1所示,当点F交在CD上时,由角平分线性质可知∠ABE=∠EBC,AD∥BC可得∠AEB=∠EBG,,即可证明AB=AE=3,BE=![]() ,同理可得BE=BG=
,同理可得BE=BG=![]() ,因AD∥BG,所以△EDF∽△GCF,设CG=x根据相似三角形的性质即可求出CG, BC=BG-CG.当F点交在DC的延长线上时,如图2所示,同理可得即可求出BC.
,因AD∥BG,所以△EDF∽△GCF,设CG=x根据相似三角形的性质即可求出CG, BC=BG-CG.当F点交在DC的延长线上时,如图2所示,同理可得即可求出BC.
解:①延长EF交BC点G,设CG=x,如图1所示:
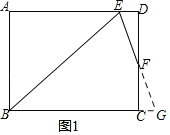
∵∠ABC的角平分线BE与AD交于点E,
∴∠ABE=∠CBE=45°,
又∵AD∥BC,
∴∠CBE=∠BEA,∠G=∠DEF
∴∠ABE=∠BEA,
∴AB=AE,
又∵AB=3,∴AE=3,
∵EF平分∠BED,
∴∠BEG=∠DEF
又∵∠G=∠DEF,
∴∠BEG=∠G
∴BG=BE
在Rt△ABE中,由勾股定理得:
![]()
∴BE=![]() ,BG=
,BG=![]() ,
,
在△DEF和△CFG中,
![]() ,
,
∴△DEF∽△CFG
∴![]() ,
,
又∵CF=1,CF+DF=CD=AB,
∴DF=2,
∴ED=2x,
又∵AD=BC,AD=AE+DE,
∴BC=3+2x,
又∵BG=BC+CG,
∴BG=3+2x+x=3+3x,
∴3+3x=![]() ,
,
x=![]() .
.
∴BC=![]() ,
,
②延长EH交DC的延长线于点F,设CH=y,如图2所示:

∵四边形ABCD是矩形,
∴AD∥BC
∴∠2=∠3,∠CBE=∠AEB,
又∵BF平分∠BED,
∴∠1=∠2,
∴∠1=∠3,
∴BE=BH,
又∵BE是∠ABC的角平分线,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
在Rt△ABE中,AB=3,由勾股定理得:
![]() ,
,
∴BH=![]() ;
;
又∵CH∥ED,
∴△FCH∽△FDE,
∴![]() ,
,
又∵CF=1,CH=y,
∴DE=4y,
又∵AD=BC,AD=AE+DE,BC=BH+CH,
∴3+4y=![]() ,
,
解得:y=![]() ,
,
∴BC=![]() ;
;
故答案为:![]() 或
或![]()