题目内容
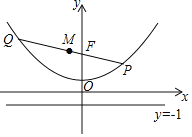
【题目】已知点P是抛物线![]() 上的任意一点,设点P到直线y=﹣1的距离为d1,点P到点F(0,3)的距离为d2
上的任意一点,设点P到直线y=﹣1的距离为d1,点P到点F(0,3)的距离为d2
(1)求抛物线的顶点坐标和对称轴;
(2)判断d1,d2的大小关系并证明;
(3)若线段PF的延长线交抛物线于点Q,且线段PQ的长度是m,线段PQ的中点M到x轴的距离是n.直接写出m与n关系式.
【答案】(1)抛物线的顶点坐标是:(0,1),对称轴为y轴;(2)d1=d2,见解析;(3)m=2n+2.
【解析】
(1)抛物线的解析式是已知的,根据顶点坐标公式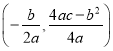 ,即可求解.
,即可求解.
(2)设P(m,![]() m2+1),分别得出d1和d2的平方值,通过比较即可得出d1和d2的大小关系.
m2+1),分别得出d1和d2的平方值,通过比较即可得出d1和d2的大小关系.
(3)作QS⊥x轴,PR⊥x轴,取RS中点N,连接MN,那么MN就是梯形PRSQ的中位线,即可得出2MN=QS+PR,从而得出m和n的关系.
解:(1)∵抛物线的解析式为:![]() ,
,
∴抛物线的顶点坐标是:(0,1),对称轴为y轴;
(2)设P(m,![]() m2+1)
m2+1)
则d12=(![]() m2+2)2=
m2+2)2=![]()
d22=m2+(3﹣![]() m2﹣1)2=
m2﹣1)2=![]()
∴d12=d22
∵d1>0,d2>0
∴d1=d2;
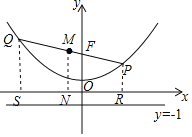
(3)作QS⊥x轴,PR⊥x轴,取RS中点N,连接MN,
同(2)可证得QS=QF﹣1,PR=PF﹣1,
由梯形中位线:2MN=QS+PR=QF﹣1+PF﹣1=QP﹣2,
则2n=m﹣2,
所以m=2n+2.

练习册系列答案
相关题目