ћвƒњƒЏ»Ё
°Њћвƒњ°њƒ≥ЌжЊя≥Іљ”µƒ600ЉюЌжЊяµƒґ©µ•Їу£ђЊцґ®”…Љ„°Ґ““Ѕљ≥µЉдє≤ЌђЌк≥……ъ≤ъ»ќќс£ђ“—÷™Љ„≥µЉдє§„ч–І¬ «““≥µЉдµƒ2±ґ£ђ““≥µЉдµ•ґјЌк≥…іЋѕо…ъ≤ъ»ќќс±»Љ„≥µЉдµ•ґјЌк≥…ґа”√10ћм£Ѓ
£®1£©«уЉ„£ђ““Ѕљ≥µЉд∆љЊщ√њћмЄчƒ№÷∆„чґа…ўЉюЌжЊя£ї
£®2£©Ѕљ≥µЉдЌђ ±њ™є§3ћмЇу£ђЅў ±”÷‘цЉ”ЅЋ90ЉюµƒЌжЊя…ъ≤ъ»ќќс£ђќ™ЅЋ єЌк≥…»ќќсµƒ„№ ±Љд≤ї≥ђєэ7ћм£ђЅљ≥µЉді”µЏ4ћм∆рЄч„‘ћбЄяє§„ч–І¬ £ђћбЄяє§„ч–І¬ ЇуЉ„≥µЉдє§„ч–І¬ »‘ «““≥µЉдє§„ч¬ µƒ2±ґ£ђ«у““≥µЉдћбЄя–І¬ Їу√њћм÷Ѕ…ў…ъ≤ъґа…ўЉюЌжЊя£Ѓ
°Њір∞Є°њ£®1£©Љ„≥µЉд∆љЊщ√њћмƒ№÷∆„ч60ЉюЌжЊя£ђ““≥µЉд∆љЊщ√њћмƒ№÷∆„ч30ЉюЌжЊя£ї£®2£©““≥µЉдћбЄя–І¬ Їу√њћм÷Ѕ…ў…ъ≤ъ35ЉюЌжЊя
°Њљвќц°њ
£®1£©…и““≥µЉд∆љЊщ√њћмƒ№÷∆„чxЉюЌжЊя£ђ‘тЉ„≥µЉд∆љЊщ√њћмƒ№÷∆„ч2xЉюЌжЊя£ђЄщЊЁє§„ч ±Љд£љє§„ч„№Ѕњ°¬є§„ч–І¬ љбЇѕ““≥µЉдµ•ґјЌк≥…іЋѕо…ъ≤ъ»ќќс±»Љ„≥µЉдµ•ґјЌк≥…ґа”√10ћм£ђЉіњ…µ√≥цєЎ”ЏxµƒЈ÷ љЈљ≥ћ£ђљв÷ЃЊ≠Љм—йЇуЉіњ…µ√≥цљб¬џ£ї
£®2£©…и““≥µЉдћбЄя–І¬ Їу√њћм…ъ≤ъmЉюЌжЊя£ђ‘тЉ„≥µЉдћбЄя–І¬ Їу√њћм…ъ≤ъ2mЉюЌжЊя£ђЄщЊЁЉ„≥µЉд∆яћм…ъ≤ъµƒЌжЊя эЉ”…ѕ““≥µЉд∆яћм…ъ≤ъµƒЌжЊя э≤ї…ў”Џґ©µ• э£ђЉіњ…µ√≥цєЎ”Џmµƒ“ї‘™“їіќ≤їµ» љ£ђљв÷Ѓ»°∆д÷–µƒ„о–°÷µЉіњ…µ√≥цљб¬џ£Ѓ
љв£Ї£®1£©…и““≥µЉд∆љЊщ√њћмƒ№÷∆„чxЉюЌжЊя£ђ‘тЉ„≥µЉд∆љЊщ√њћмƒ№÷∆„ч2xЉюЌжЊя£ђ
“јћв“в£ђµ√£Ї![]() £ђ
£ђ
љвµ√£Їx£љ30£ђ
Њ≠Љм—й£ђx£љ30 «‘≠Јљ≥ћµƒљв£ђ«“ЈыЇѕћв“в£ђ
°а2x£љ60£Ѓ
ір£ЇЉ„≥µЉд∆љЊщ√њћмƒ№÷∆„ч60ЉюЌжЊя£ђ““≥µЉд∆љЊщ√њћмƒ№÷∆„ч30ЉюЌжЊя£Ѓ
£®2£©…и““≥µЉдћбЄя–І¬ Їу√њћм…ъ≤ъmЉюЌжЊя£ђ‘тЉ„≥µЉдћбЄя–І¬ Їу√њћм…ъ≤ъ2mЉюЌжЊя£ђ
“јћв“в£ђµ√£Ї60°Ѕ3+£®7©Б3£©°Ѕ2m+30°Ѕ3+£®7©Б3£©m°Ё600+90£ђ
љвµ√£Їm°Ё35£Ѓ
ір£Ї““≥µЉдћбЄя–І¬ Їу√њћм÷Ѕ…ў…ъ≤ъ35ЉюЌжЊя£Ѓ

°Њћвƒњ°њƒ≥∞а°∞ э—І–Ћ»§–°„й°±ґ‘Їѓ э![]() µƒЌЉѕсЇЌ–‘÷ љш––ЅЋћљЊњ£ђћљЊњєэ≥ћ»зѕ¬£ђ«л≤є≥дЌк’ы£Ѓ
µƒЌЉѕсЇЌ–‘÷ љш––ЅЋћљЊњ£ђћљЊњєэ≥ћ»зѕ¬£ђ«л≤є≥дЌк’ы£Ѓ
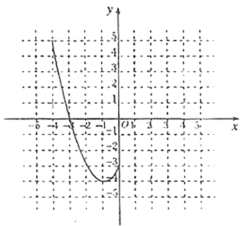
£®1£©„‘±дЅњ![]() µƒ»°÷µЈґќІ «»Ђће µ э£ђ
µƒ»°÷µЈґќІ «»Ђће µ э£ђ![]() ”л
”л![]() µƒЉЄ„йґ‘”¶÷µЅ–±н»зѕ¬£Ї
µƒЉЄ„йґ‘”¶÷µЅ–±н»зѕ¬£Ї
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆д÷–£ђ![]() ________________£Ѓ
________________£Ѓ
£®2£©ЄщЊЁ…ѕ±н эЊЁ£ђ‘Џ»зЌЉЋщ Њµƒ∆љ√ж÷±љ«„ш±кѕµ÷–√иµг£ђ≤Ґї≠≥цЅЋЇѓ эЌЉѕсµƒ“ї≤њЈ÷£ђ«лї≠≥цЄ√ЌЉѕсµƒЅн“ї≤њЈ÷£ї
£®3£©єџ≤мЇѓ эЌЉѕс£ђ–і≥цЅљћхЇѓ эµƒ–‘÷ £ї
£®4£©љш“ї≤љћљЊњЇѓ эЌЉѕсЈҐѕ÷£Ї
ҐўЈљ≥ћ![]() ”–______Єц µ эЄщ£ї
”–______Єц µ эЄщ£ї
ҐЏЇѓ эЌЉѕс”л÷±ѕя![]() ”–_______Єцљїµг£ђЋщ“‘ґ‘”¶Јљ≥ћ
”–_______Єцљїµг£ђЋщ“‘ґ‘”¶Јљ≥ћ![]() ”–_____Єц µ эЄщ£ї
”–_____Єц µ эЄщ£ї
ҐџєЎ”Џ![]() µƒЈљ≥ћ
µƒЈљ≥ћ![]() ”–
”–![]() Єц µ эЄщ£ђ
Єц µ эЄщ£ђ![]() µƒ»°÷µЈґќІ «___________£Ѓ
µƒ»°÷µЈґќІ «___________£Ѓ