题目内容
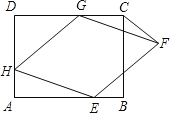
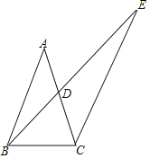
【题目】如图，在△ABC中，AB＝AC，点D为AC中点，点E在BD延长线上，且BD：DE＝3：5，连接CE，tan∠BAC＝
，CB＝
，则线段EC长为_____．
【答案】
【解析】
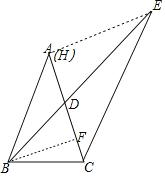
如图，作BF⊥AC于F，EH⊥AC于H．由tan∠BAF＝
，可设BF＝3k，AF＝4k，则AC、CF、DF都可以用k的代数式表示，易证△EHD∽△BFD，进而可得点H与点A重合，AE＝AC，由此可推出EC＝
AC，然后在直角△BCF中利用勾股定理构建方程，求出k即可解决问题．
解：如图，作BF⊥AC于F，EH⊥AC于H．
∵tan∠BAF＝，∴设BF＝3k，AF＝4k，则AB＝AC＝5k，
∴CF＝k，AD=CD=2.5k，∴DF＝2.5k－k=1.5k，
∵∠EHD＝∠BFD＝90°，∠EDH＝∠BDF，∴△EHD∽△BFD，
∴
，即
，
∴DH＝2.5k，EH＝5k，
∵AD＝DC＝2.5k，∴DA＝DH，∴点H与点A重合，
∵AC＝AE＝5k，∴EC＝AE＝5k，
∵BC＝
，解得：k＝
，
∴EC＝
．
故答案为．
练习册系列答案
相关题目
