题目内容
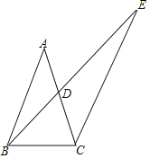
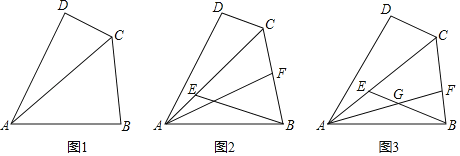
【题目】如图1,四边形ABCD中,对角线AC平分∠DCB,且AD=AB,CD<CB
(1)求证:∠B+∠D=180°;
(2)如图2,在AC上取一点E,使得BE∥CD,且BE=CE,点F在线段BC上,连接AF,且AB=AF,求证:AE=CF;
(3)如图3,在(2)的条件下,若BE与AF交于点G,BF:AB=2:7,求tan∠BGF的值.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)如图4中,作AE⊥BC于E,作AF⊥CD交CD的延长线于F,先根据AAS证明△ACF≌△ACE,推出AF=AE,再根据HL证明Rt△AFD≌Rt△AEB,可得∠ADF=∠B,进一步即可证得结论;
(2)如图5中,作AM∥EB交CB的延长线于M,利用平行线的性质和等腰三角形的性质可证得∠CEB=∠ECB=∠EBC,则△BCE是等边三角形,进一步即可证得△ACM也是等边三角形,进而可得AE=BM,然后根据AAS可证明△ACF≌△AMB,可得CF=BM,继而可得结论;
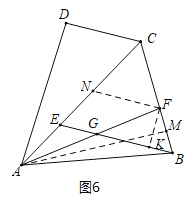
(3)如图6中,作AM⊥BC于M,FK⊥BE于K,FN∥BE交AC于N.设BF=2a,AB=7a,进而可用a的代数式依次表示出FM、BM、AM、CM,易证△CNF是等边三角形,进一步即可表示出FN、EN,易得△AEG∽△ANF,然后利用相似三角形的性质即可用含a的代数式表示出EG,进而可得GB,而在直角△BFK中,FK、BK易得,问题即得解决.
解:(1)证明:如图4中,作AE⊥BC于E,作AF⊥CD交CD的延长线于F.
∵∠AFC=∠AEC=90°,∠ACF=∠ACE,AC=AC,
∴△ACF≌△ACE(AAS),∴AF=AE,
∵AD=AB,∠F=∠AEB=90°,
∴Rt△AFD≌Rt△AEB(HL),∴∠ADF=∠B,
∵∠ADF+∠ADC=180°,∴∠ADC+∠B=180°;
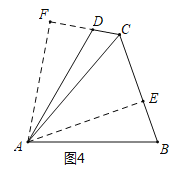
(2)证明:如图5中,作AM∥EB交CB的延长线于M.
∵BE=EC,∴∠ECB=∠EBC,
∵CD∥BE,∴∠DCE=∠CEB,
∵∠DCE=∠ECB,
∴∠CEB=∠ECB=∠EBC=60°,
∴△ECB是等边三角形,
∵EB∥AM,∴∠CEB=∠CAB=60°,∠CBE=∠M=60°,
∴△ACM是等边三角形,∴CA=CM,
∵CE=CB,∴AE=BM,
∵AF=AB,∴∠AFB=∠ABF,∴∠AFC=∠ABM,
又∵AC=AM,∠ACF=∠M=60°,
∴△ACF≌△AMB(AAS),
∴CF=BM,∴AE=CF;

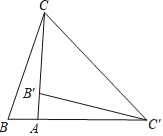
(3)解:如图6中,作AM⊥BC于M,FK⊥BE于K,FN∥BE交AC于N.
∵FB:AB=2:7,∴设BF=2a,AB=7a,
∵AF=AB,AM⊥BF,∴FM=BM=a,
∴AM=![]() ,
,
∵∠ACM=60°,∴AM=![]() CM,∴CM=4a,CF=AE=CM-FM=3a,
CM,∴CM=4a,CF=AE=CM-FM=3a,
∵FN∥BE,∴∠CNF=∠CEB=60°,∠CFE=∠CBE=60°,∴△CNF是等边三角形,
∴CF=CN=FN=3a,EN=BF=2a,AN=AE+EN=5a,
∵EG∥FN,∴△AEG∽△ANF,∴![]() ,即
,即![]() ,
,
∴EG=![]() a,BG=EB﹣EG=5a﹣
a,BG=EB﹣EG=5a﹣![]() a=
a=![]() a,
a,
在Rt△BFK中,∵BF=2a,∠FBK=60°,∴BK=a,FK=![]() a,
a,
∴GK=BG﹣BK=![]() a﹣a=
a﹣a=![]() a,
a,
∴tan∠FGB=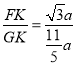 =
=![]() .
.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案