Question

【题目】数学概念

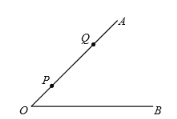
若点在的内部，且、和中有两个角相等，则称是的“等角点”，特别地，若这三个角都相等，则称是的“强等角点”.

理解概念

（1）若点是的等角点，且，则的度数是 .

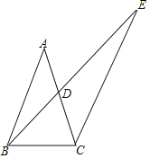
（2）已知点在的外部，且与点在的异侧，并满足，作的外接圆，连接，交圆于点.当的边满足下面的条件时，求证：是的等角点.（要求：只选择其中一道题进行证明！）

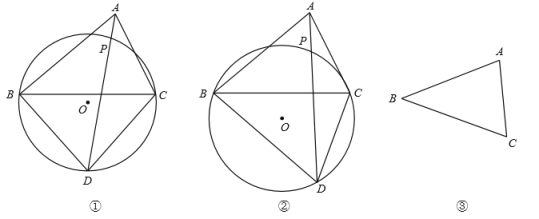
①如图①，

②如图②，

深入思考

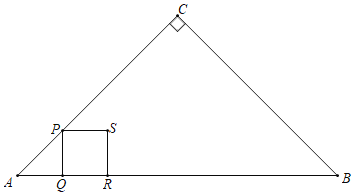
（3）如图③，在中，、、均小于，用直尺和圆规作它的强等角点.（不写作法，保留作图痕迹）

（4）下列关于“等角点”、“强等角点”的说法：

①直角三角形的内心是它的等角点；

②等腰三角形的内心和外心都是它的等角点；

③正三角形的中心是它的强等角点；

④若一个三角形存在强等角点，则该点到三角形三个顶点的距离相等；

⑤若一个三角形存在强等角点，则该点是三角形内部到三个顶点距离之和最小的点，其中正确的有 .（填序号）

Answer 1

【答案】（1）100、130或160；（2）选择①或②，理由见解析；（3）见解析；（4）③⑤

【解析】

（1）根据“等角点”的定义，分类讨论即可；

（2）①根据在同圆中，弧和弦的关系和同弧所对的圆周角相等即可证明；

②弧和弦的关系和圆的内接四边形的性质即可得出结论；

（3）根据垂直平分线的性质、等边三角形的性质、弧和弦的关系和同弧所对的圆周角相等作图即可；

（4）根据“等角点”和“强等角点”的定义，逐一分析判断即可．

（1）（i）若=时，

∴==100°

（ii）若时，

∴（360°－）=130°；

（iii）若=时，

360°－－=160°，

综上所述：=100°、130°或160°

故答案为：100、130或160．

（2）选择①：

连接

∵

∴

∴

∵，

∴

∴是的等角点．

选择②

连接

∵

∴

∴

∵四边形是圆的内接四边形，

∴

∵

∴

∴是的等角点

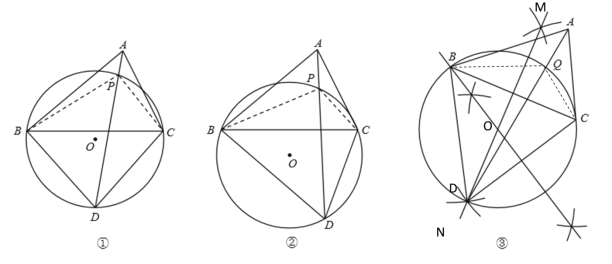
（3）作BC的中垂线MN，以C为圆心，BC的长为半径作弧交MN与点D，连接BD，

根据垂直平分线的性质和作图方法可得：BD=CD=BC

∴△BCD为等边三角形

∴∠BDC=∠BCD=∠DBC=60°

作CD的垂直平分线交MN于点O

以O为圆心OB为半径作圆，交AD于点Q，圆O即为△BCD的外接圆

∴∠BQC=180°－∠BDC=120°

∵BD=CD

∴∠BQD=∠CQD

∴∠BQA=∠CQA=（360°－∠BQC）=120°

∴∠BQA=∠CQA=∠BQC

如图③，点即为所求．

（4）③⑤．

①如下图所示，在RtABC中，∠ABC=90°，O为△ABC的内心

假设∠BAC=60°，∠ACB=30°

∵点O是△ABC的内心

∴∠BAO=∠CAO=∠BAC=30°，∠ABO=∠CBO=∠ABC=45°，∠ACO=∠BCO=∠ACB=15°

∴∠AOC=180°－∠CAO－∠ACO=135°，∠AOB=180°－∠BAO－∠ABO=105°，∠BOC=180°－∠CBO－∠BCO=120°

显然∠AOC≠∠AOB≠∠BOC，故①错误；

②对于钝角等腰三角形，它的外心在三角形的外部，不符合等角点的定义，故②错误；

③正三角形的每个中心角都为：360°÷3=120°，满足强等角点的定义，所以正三角形的中心是它的强等角点，故③正确；

④由（3）可知，点Q为△ABC的强等角，但Q不在BC的中垂线上，故QB≠QC，故④错误；

⑤由（3）可知，当的三个内角都小于时，必存在强等角点．

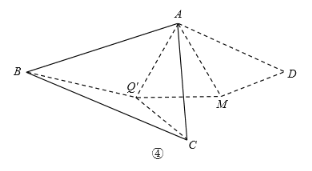
如图④，在三个内角都小于的内任取一点，连接、、，将绕点逆时针旋转到，连接，

∵由旋转得，，

∴是等边三角形．

∴

∴

∵、是定点，

∴当、、、四点共线时，最小，即最小．

而当为的强等角点时，，

此时便能保证、、、四点共线，进而使最小．

故答案为：③⑤．