题目内容
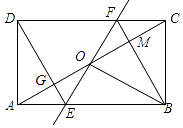
【题目】已知:△ABC是等腰直角三角形.∠A=90°,CE平分∠ACB交AB于点E.
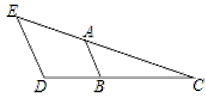
(1)如图1,若点D在斜边BC上,DM垂直平分BE,垂足为M.求证:BD=AE.
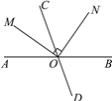
(2)如图2,过点B作BF⊥CE交CE的延长线于点F.若CE=6,求△BEC的面积.

【答案】(1)见解析;(2)9
【解析】
(1)由∠BAC=90°,AB=AC,可得∠B=45°,由DM垂直平分BE,可得BD=DE,进而判断△BDE是等腰直角三角形,所以ED⊥BD,然后由角平分线的性质可得ED=AE,根据等量代换可得BD=AE;
(2)延长BF,CA,交与点G,由CE平分∠ACB,可得∠ACE=∠BCE,由BF⊥CE,可得∠BFC=∠GFC=90°,然后由三角形内角和定理可得:∠GBC=∠G,进而可得BC=GC,然后由等腰三角形的三线合一,可得BF=FG=![]() BG,所以BG=2BF=2FG=4,然后再由ASA,可证△ACE≌△ABG,可得EC=BG=4,最后根据三角形的面积公式即可求△BEC的面积.
BG,所以BG=2BF=2FG=4,然后再由ASA,可证△ACE≌△ABG,可得EC=BG=4,最后根据三角形的面积公式即可求△BEC的面积.
解:(1)∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵DM垂直平分BE,
∴BD=ED,
∴∠BED=∠B=45°,
∴∠EDC=∠B+∠BED=90°,
∵CE平分∠ACB,∠BAC=90°,∠EDC=90°,
∴ED=EA,
∴BD=AE;
(2)延长BF和CA交于点G,如图,
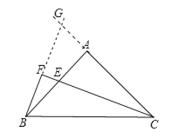
∵CE平分∠ACB,∴∠ACF=∠BCF,
∵BF⊥CE,∴∠BFC=∠GFC=90°,
∴∠CBG=∠CGB,∴CG=CB,
∴BF=GF=![]() BG,
BG,
∵∠GFC=∠GAB=90°,∴∠ACF+∠G=90°,
∴∠ABG+∠G=90°,∴∠ACF=∠ABG,
在△ACE和△ABG中,
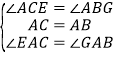 ,
,
∴△ACE≌△ABG(ASA),
∴CE=BG,
∴CE=2BF,
∵CE=6,
∴BF=![]() CE=3,
CE=3,
S△BEC=![]() CEBF=
CEBF=![]() ×6×3=9.
×6×3=9.

 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案