Question

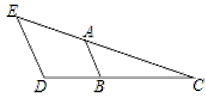
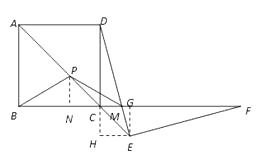
【题目】如图1，在正方形ABCD中，P在对角线AC上，E在AC的延长线上，PB＝PM ， DE＝EF.

（1）求证：∠CDE＝∠F；
（2）若AB＝5，CM＝1，求PB的长；
（3）如图2，若BF＝10，△QCF是以CF为底的等腰三角形，连接DQ ， 试求△CDQ的最大面积.

Answer 1

【答案】
（1）

过E作EG⊥CF于G，EH⊥DC于H

则四边形CHEG是矩形，

∵四边形ABCD是正方形，

∴∠ACB＝∠ACD＝45°，

∴∠ECG＝∠ECH＝45°，

∴CH=EH

∵矩形CHEG是正方形

∴EG＝EH

又∵DE＝EF，∴Rt△DEH≌Rt△FEG

∴∠CDE＝∠F

（2）

解：过P作PN⊥BC于N

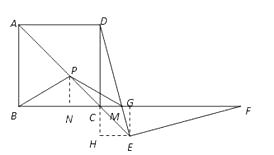
∵BC＝AB＝5，CM＝1，∴BM＝6

∵PB＝PM，∴BN＝NM＝3，

∴NC＝2

在Rt△PNC中，∵∠PCN＝45°，

∴PN＝NC＝2

在Rt△PNM中，PM＝ ＝ ＝ ，

∴PB＝

（3）

作QR⊥CF于R，QK⊥CD于K

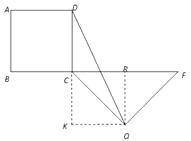
则四边形CKQR是矩形，

∴KQ＝CR

又∵△QCF是以CF为底的等腰三角形，∴ CR=RF=CF

设BC＝x，则CD＝x，

KQ＝CR＝CF＝(10－x)＝5－x

∴S△CDQ＝CD·KQ＝·x·(5－x)

＝－x2＋ x＝－(x－5)2＋

∴当x＝5，△CDQ的面积有最大值

【解析】
【考点精析】掌握等腰三角形的性质和勾股定理的概念是解答本题的根本，需要知道等腰三角形的两个底角相等（简称：等边对等角）；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．