题目内容
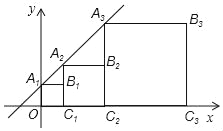
【题目】如图，抛物线y=ax-2ax-3a（a＜0）与x轴交于A、B两点（A在B的左侧），与y轴交于点C，抛物线的对称轴与抛物线交于点P，与直线BC交于点M，且PM= 
AB.
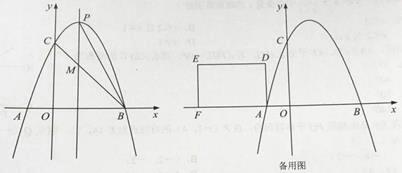
（1）求抛物线的解析式；
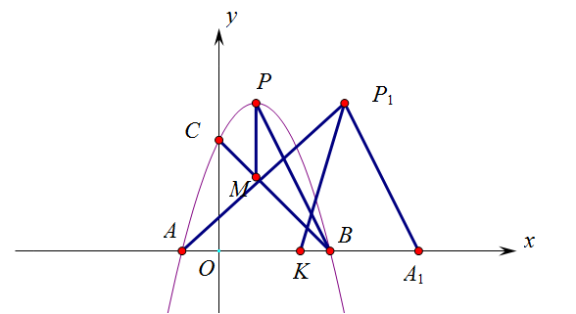
（2）点K是x轴正半轴上一点，点A、P关于点K的对称点分别为 
、 
，连接 
、 
，若 
，求点K的坐标；
（3）矩形ADEF的边AF在x轴负半轴上，边AD在第二象限，AD=2，DE=3.将矩形ADEF沿x轴正方向平移t（t＞0）个单位，直线AD、EF分别交抛物线于G、H.问：是否存在实数t，使得以点D、F、G、H为顶点的四边形是平行四边形？若存在，求出t的值；若不存在，说明理由.
【答案】
（1）
解：由抛物线y=ax-2ax-3a可得它的顶点坐标为（1，-4a）.
当x=0时，y=3a，则C（0，-3a）
当y=0时，
则ax-2ax-3a=0，则x1=-1，x2=3.
则A（-1,0），B（3,0）.
即AB=4.
由B（3,0）和C（0,-3a）可得直线BC的解析式为y=ax-3a，
则M（1,-2a）,
则pM=-2a=2，即a=-1，
所以抛物线的解析式为y=-x+2x+3.
（2）
解：如图，连接KP1，设K（m，0），m>0，
则P1（2m-1，4），A1（2m+1，0），
当 P1A⊥P1A1时，KP1=AK，
则（2m-1-m）2+42=(m+1)2，
解得m=4.
则K（4,0）.
（3）
解：由题可得DG//FH，当DG=FH时，以点D、F、G、H为顶点的四边形是平行四边形.
因为G是直线AD与抛物线的交点，则G（-1+t，-（-1+t）2+2(-1+t)+3），即（-1+t，-t2+4t）
同理H（-4+t，-（-4+t）2+2（-4+t）+3），即H（-4+t，-t2+10t-21），
则DG=|2-(-t2+4t)|=|t2-4t+2|，
FH=|-t2+10t-21|，
当DG=FH时，
则t2-4t+2=-t2+10t-21或t2-4t+2=-（-t2+10t-21），
解得t=
或t=，
【解析】（1）由抛物线y=ax-2ax-3a可分别求出点P，C，B，A的坐标，则可求出AB的值，求出BC的解析式，从而得到点M的坐标，PM的长度，由PM=
AB，可求得a；
（2）根据对称的性质得到点P1的坐标，由当 P1A⊥P1A1时，KP1=AK，列方程解出m即可；
（3）由题可得DG//FH，当DG=FH时，以点D、F、G、H为顶点的四边形是平行四边形，则分别求出DG和FH的值，列方程即可解得.
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．
