题目内容
【题目】第一象限内两点![]() ,
,![]() ,点P在x轴上,若
,点P在x轴上,若![]() 最小,则Р点坐标为________.
最小,则Р点坐标为________.
【答案】![]()
【解析】
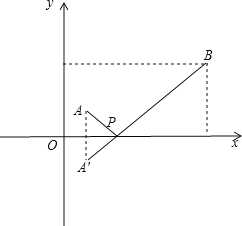
先画出图形,由两点之间线段最短可知,作出A点对称点,连接A'B交x轴于一点,此点就是点P,即PA+PB=A'B,此时PA+PB最小,求得直线A'B的解析式为y=x﹣2,当y=0时,x=2,即可得到结论.
作点A关于x轴的对称点A',则A'坐标为(1,﹣1),
连接A'B交x轴于一点,此点就是点P,此时PA+PB最小,
作BE⊥y于一点E,延长A'A交BE于一点M.
∵PB=PA',∴PA+PB=BA'.
∵A、B两点的坐标分别为(1,1)和(5,3),A'坐标为(1,﹣1),
设直线A'B的解析式为:y=kx+b,
∴![]() ,解得:
,解得:![]() ,
,
∴直线A'B的解析式为:y=x﹣2,
当y=0时,x=2,∴P(2,0).
故答案为:(2,0).

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目