题目内容
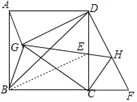
【题目】如图,矩形ABCD中,点E在AD边上,过点E作AB的平行线,交BC于点F,将矩形ABFE绕着点E逆时针旋转,使点F的对应点落在边CD上,点B的对应点N落在边BC上.
(1)求证:BF=NF;
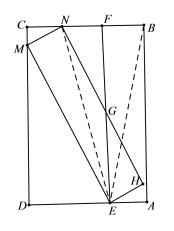
(2)已知AB=2,AE=1,求EG的长;
(3)已知∠MEF=30°,求![]() 的值.
的值.
【答案】(1)详见解析;(2)EG=![]() ;(3)
;(3)![]() .
.
【解析】
(1)连结BE,EN,根据旋转的性质可知BE=EN,由∠EFB=90°,根据等腰三角形底边的高是底边中线即可证明BF=NF.(2)根据旋转的性质可证明△NGF≌△HGE,进而证明FG=GH,根据勾股定理求出GE的长即可.(3)根据EF//CD可知∠MEF=DME=30°,由旋转性质可知∠EMN=90°,进而可知∠CNM=30°,设DE=x,则ME=2x,MD=![]() x,进而可求出CM的长,即可求出MN的长,根据BC=DE+MN即可求出BC的长,进而求出答案.
x,进而可求出CM的长,即可求出MN的长,根据BC=DE+MN即可求出BC的长,进而求出答案.
(1)连结BE,EN,如图,
∵四边形ABCD是矩形,
∴∠BFE=90°,
由旋转得BE=EN,
∴BF=NF;
(2)∵四边形ABCD是矩形,
∴BF=AE,EF=AB,
由旋转得EH=EA,
∵BF=NF,
∴EH=NF,
∵∠BFE=∠GHE=90°,∠NGF=∠HGE,
∴△NGF≌△HGE,
∴FG=GH,
设GE=x,则GF=GH=2﹣x,
由勾股定理得x2﹣(2﹣x)2=1,
解得x=![]() ,
,
∴EG=![]() ;
;
(3)∵EF∥DC,
∴∠DME=∠MEF=30°,
设DE=x,
∵∠D=90°,
∴ME=DC=AB=2x,DM=![]() x,
x,
∴MC=(2﹣![]() )x,
)x,
∵∠NME=90°,∠DME=30°,
∴∠NMC=60°,
∴∠MNC=30°,
∴MN=2MC=2(2﹣![]() )x,
)x,
∴BC=AD=DM+MN=2(2﹣![]() )x+x=(5﹣2
)x+x=(5﹣2![]() )x,
)x,
∴![]() =
=![]() .
.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示:

(1)根据图示填写下表:
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 |
|
|
高中部 | 85 |
|
|
(2)结合两队成绩的平均数中中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手的成绩较为稳定.