题目内容
【题目】在菱形ABCD中,AC是对角线.
(1)如图①,若AB=6,则菱形ABCD的周长为______;若∠DAB=70,则∠D的度数是_____;∠DCA的度数是____;
(2)如图②,P是AB上一点,连接DP交对角线AC于点E,连接EB,求证: ∠APD=∠EBC.

【答案】(1)24;110°;35°;(2)见解析.
【解析】
(1)由菱形的性质可求解;
(2)由“SAS”可得△DCE≌△BCE,可得∠CDP=∠CBE,由平行线的性质可得∠CDP=∠APD=∠CBE.
解:(1)∵四边形ABCD是菱形
∴AB=BC=CD=AD=6,∠DAB+∠ADC=180°,
∠DCA=![]() ∠DCB=
∠DCB=![]() ∠DAB=35°
∠DAB=35°
∴菱形ABCD的周长=4×6=24,
∠ADC=180°-70°=110°,
故答案为:24,110°,35°
(2)证明:∵菱形ABCD
∴CD//AB,CD=CB,CA平分∠BCD
∴∠CDE=∠APD,∠ACD=∠ACB
∵CD=CB,∠BCE=∠DCE,CE=CE
∴△CBE≌△CDE(SAS)
∴∠CBE=∠CDE
∴∠CBE=∠APD.

练习册系列答案
相关题目
【题目】(10分)下面的图形是由边长为l的正方形按照某种规律排列而组成的.
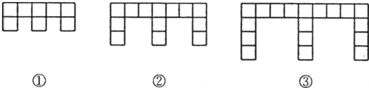
(1)观察图形,填写下表:
图形 | ① | ② | ③ |
正方形的个数 | 8 |
|
|
图形的周长 | 18 |
|
|
(2)推测第n个图形中,正方形的个数为 ,周长为 (都用含n的代数式表示).
(3)这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系可表示为y= .
【题目】某种水果的价格如表:
购买的质量(千克) | 不超过10千克 | 超过10千克 |
每千克价格 | 6元 | 5元 |
张欣两次共购买了25千克这种水果(第二次多于第一次),共付款132元.问张欣第一次、第二次分别购买了多少千克这种水果?