Question

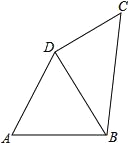
【题目】已知：如图，在△ABC中，AB=AC，点D、E分别在AB、AC上，

（1）若∠BDO=∠CEO，求证：BE=CD．

（2）若点E为AC中点，问点D满足什么条件时候，．

Answer 1

【答案】（1）详见解析；（2）详见解析.

【解析】分析：

（1）由AB=AC可得∠ABC=∠ACB，结合∠BDO=∠CEO和BC=CB可得△DBC≌△ECB，由此可得BE=CD；

（2）由E为AC中点可知，若此时D为AB的中点，则由三角形中位线定理可得DE∥BC，DE=BC，从而可得△DEO∽△BCO，由此即可得到.

详解：

（1）∵AB=AC，

∴∠ABC=∠ACB，

在△DBC与△ECB中， ，

∴△DBC≌△ECB，

∴BE=CD；

（2）当点D为AB的中点时，，理由如下：
∵点E为AC中点，点D为AB的中点，

∴DE=BC，DE∥BC，

∴△DEO∽△BCO，

∴.