题目内容
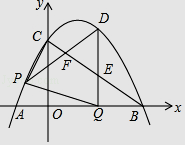
【题目】如图,在平面直角坐标系中点A(![]() ,
, ![]() ),B(2
),B(2![]() ,0),点C为线段OB上一个动点,以AC为腰作等腰直角△ACD,且AC=AD.
,0),点C为线段OB上一个动点,以AC为腰作等腰直角△ACD,且AC=AD.
(1)△AOB的面积;
(2)证明:OC2+CB2=CD2.
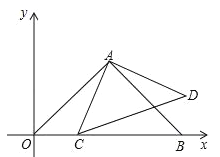
【答案】(1)S△AOB=3;(2)见解析
【解析】试题分析:(1)根据题意可知A(![]() ,
, ![]() ),B(2
),B(2![]() ,0),利用三角形的面积公式直接求解即可;(2)连接BD,根据题意求得OA=AB=
,0),利用三角形的面积公式直接求解即可;(2)连接BD,根据题意求得OA=AB=![]() ,根据勾股定理的逆定理判定三角形AOB为等腰直角三角形,再利用SAS判定△OAC≌△BAD,根据全等三角形的性质可得OC=BD,,∠AOC=∠ABD=45°,即可得∠CBD=90°,再由勾股定理即可得结论.
,根据勾股定理的逆定理判定三角形AOB为等腰直角三角形,再利用SAS判定△OAC≌△BAD,根据全等三角形的性质可得OC=BD,,∠AOC=∠ABD=45°,即可得∠CBD=90°,再由勾股定理即可得结论.
试题解析:
(1) S△AOB=![]() ×2
×2![]() ×
×![]() =3;
=3;
(2)证明:连接BD,
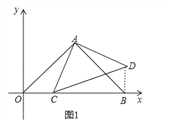
由题意得OA=AB=![]() ,
,
∵OA=AB=![]() ,OB=2
,OB=2![]() ,
,
∴OA2+OB2=OB2,
∴∠OAB=90°,∠AOB=∠ABO=45°,
∵∠OAB=∠CAD,
∴∠OAC=∠BAD,
∵∠AO=AB,AC=AD,
∴△OAC≌△BAD,
∴OC=BD,∠AOC=∠ABD=45°,
∴∠CBD=90°,
∴CD2=BC2+BD2.

练习册系列答案
相关题目