题目内容
【题目】如图,抛物线y=﹣ ![]() x2+
x2+ ![]() x+3
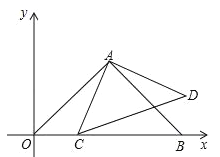
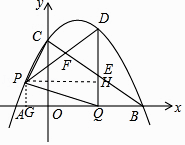
x+3 ![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).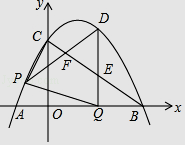
(1)求直线BC的函数表达式;
(2)①直接写出P,D两点的坐标(用含t的代数式表示,结果需化简)
②在点P、Q运动的过程中,当PQ=PD时,求t的值;
(3)试探究在点P,Q运动的过程中,是否存在某一时刻,使得点F为PD的中点?若存在,请直接写出此时t的值与点F的坐标;若不存在,请说明理由.
【答案】
(1)
解:由y=0得﹣ ![]() x2+
x2+ ![]() x+3
x+3 ![]() =0,
=0,
解得:x1=﹣3,x2=9,
∴B(9,0),
由x=0得y=3 ![]() ,
,
∴C(0,3 ![]() ),
),
设直线BC的解析式为y=kx+b,∴ ![]() ,
,
∴  ,
,
∴直线BC的解析式为y=﹣ ![]() x+3
x+3 ![]()
(2)
解:①过p作PG⊥x轴于G,
∵A(﹣3,0),C(0,3 ![]() ),
),
∴OA=3.OC=3 ![]() ,
,
∴tan∠CAO= ![]() ,
,
∴∠CAO=60°,
∵AP=t,
∴PG= ![]() t,AG=
t,AG= ![]() t,
t,
∴OG=3﹣ ![]() t,
t,
∴P( ![]() t﹣3,
t﹣3, ![]() t),
t),
∵DQ⊥x轴,BQ=2t,
∴OQ=9﹣2t,
∴D(9﹣2t,﹣ ![]() t2+
t2+ ![]() t),
t),
②过P作PH⊥QD于H,
则四边形PGQH是矩形,
∴HQ=PG,∵PQ=PD,PH⊥QD,∴DQ=2HQ=2PG,∵P( ![]() t﹣3,
t﹣3, ![]() t),D(9﹣2t,﹣
t),D(9﹣2t,﹣ ![]() t2+
t2+ ![]() t),
t),
∴﹣ ![]()
![]() t=2×
t=2× ![]() t,
t,
解得:t1=0(舍去),t2= ![]() ,∴当PQ=PD时,t的值是
,∴当PQ=PD时,t的值是 ![]() ;
;
(3)
解:∵点F为PD的中点,
∴F的横坐标为: ![]() (
( ![]() t﹣3+9﹣2t)=﹣
t﹣3+9﹣2t)=﹣ ![]() t+3,F的纵坐标为
t+3,F的纵坐标为 ![]() (
( ![]() t﹣
t﹣ ![]() t2+
t2+ ![]() t)=﹣
t)=﹣ ![]() t2+
t2+ ![]() t,
t,
∴F(﹣ ![]() t+3,﹣
t+3,﹣ ![]() t2+
t2+ ![]() t),
t),
∵点F在直线BC上,
∴﹣ ![]() t2+
t2+ ![]() t=﹣
t=﹣ ![]() (﹣
(﹣ ![]() t+3)+3
t+3)+3 ![]() ,
,
∴t=3,
∴F( ![]() ,
, ![]() )
)
【解析】(1)更好函数的解析式得到B(9,0),C(0,3 ![]() ),解方程组即可得到结论;(2)①过p作PG⊥x轴于G,解直角三角形得到∠CAO=60°,得到PG=
),解方程组即可得到结论;(2)①过p作PG⊥x轴于G,解直角三角形得到∠CAO=60°,得到PG= ![]() t,AG=
t,AG= ![]() t,于是得到P(
t,于是得到P( ![]() t﹣3,
t﹣3, ![]() t),把OQ=9﹣2t代入二次函数的解析式即可得到D(9﹣2t,﹣
t),把OQ=9﹣2t代入二次函数的解析式即可得到D(9﹣2t,﹣ ![]() t2+
t2+ ![]() t),②过P作PH⊥QD于H,得到四边形PGQH是矩形,列方程即可得到即可;(3)根据折叠坐标公式得到F(﹣
t),②过P作PH⊥QD于H,得到四边形PGQH是矩形,列方程即可得到即可;(3)根据折叠坐标公式得到F(﹣ ![]() t+3,﹣
t+3,﹣ ![]() t2+
t2+ ![]() t),由点F在直线BC上,列方程即可得到结论.
t),由点F在直线BC上,列方程即可得到结论.