题目内容
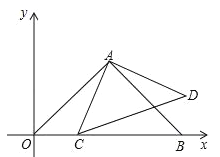
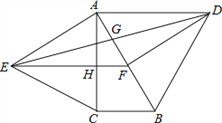
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC; ②四边形ADFE为菱形; ③AD=4AG; ④FH=![]() BD
BD
其中正确的结论有( ).
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
【答案】C
【解析】∵△ACE是等边三角形,∴∠EAC=60°,AE=AC.
∵∠BAC=30°,∴∠FAE=∠ACB=90°,AB=2BC.
∵F为AB的中点,∴AB=2AF,∴BC=AF,∴△ABC≌△EFA,∴FE=AB,
∴∠AEF=∠BAC=30°,∴EF⊥AC,故①正确,
∵EF⊥AC,∠ACB=90°,∴HF∥BC.
∵F是AB的中点, ![]() .
.
![]() ,AB=BD,
,AB=BD, ![]() ,故④说法正确;
,故④说法正确;
∵AD=BD,BF=AF,∴∠DFB=90°,∠BDF=30°.
∵∠FAE=∠BAC+∠CAE=90°,∴∠DFB=∠EAF.
∵EF⊥AC,∴∠AEF=30°,∴∠BDF=∠AEF,∴△DBF≌△EFA(AAS),∴AE=DF.
∵FE=AB,∴四边形ADFE为平行四边形.
∵AE≠EF,∴四边形ADFE不是菱形;故②说法不正确;
∵四边形ADFE为平行四边形,
![]() ,
, ![]() .
.
∵AD=AB,∴AD=4AG,故③说法正确,
所以正确的有:①③④.故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为了解某社区居民的用电情况,随机对该社区10户居民进行调查,下表是这10户居民2015年4月份用电量的调查结果:
居民(户) | 1 | 2 | 3 | 4 |
月用电量(度/户) | 30 | 42 | 50 | 51 |
那么关于这10户居民月用电量(单位:度),下列说法错误的是( )
A.中位数是50
B.众数是51
C.方差是42
D.极差是21