题目内容
【题目】(1)以a,b为直角边,c为斜边作两个全等的Rt△ABE与Rt△FCD拼成如图1所示的图形,使B,E,F,C四点在一条直线上(此时E,F重合),可知△ABE ≌△FCD,AE![]() DF,请你证明:
DF,请你证明:![]() ;
;
(2)在(1)中,固定△FCD,再将△ABE沿着BC平移到如图2的位置(此时B,F重合),请你重新证明:![]() .
.
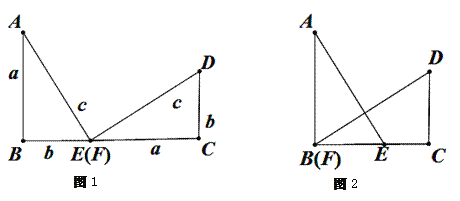
【答案】(1)如图,连接AD.
由![]()
∴![]()
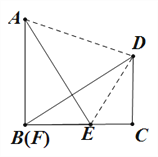
化简得![]()
连接AD,DE.
由![]()
∴![]()
化简得![]() …………8分
…………8分
【解析】试题分析:(1)连接AD,由四边形ABCD的面积=△ABE的面积+△FCD的面积+△ADE的面积,得出![]() (a+b)2=
(a+b)2=![]() ab×2+
ab×2+![]() c2,即可得出结论;
c2,即可得出结论;
(2)连接AD、DE,四边形ABCD的面积=四边形ABED的面积+△DCE的面积,得出![]() (a+b)×a=
(a+b)×a=![]() c2+
c2+![]() b(a-b),即可得出结论.
b(a-b),即可得出结论.
试题解析:(1)连接AD,如图1所示:
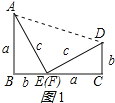
则四边形ABCD是直角梯形,
∴四边形ABCD的面积=![]() (a+b)(a+b)=12(a+b)2,
(a+b)(a+b)=12(a+b)2,
∵四边形ABCD的面积=△ABE的面积+△FCD的面积+△ADE的面积,
即![]() (a+b)2=
(a+b)2=![]() ab×2+
ab×2+![]() c2,
c2,
化简得:(a+b)2=2ab+c2,
∴a2+b2=c2;
(2)连接AD、DE,如图2所示:
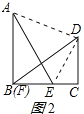
则四边形ABCD的面积=四边形ABED的面积+△DCE的面积,
即![]() (a+b)×a=
(a+b)×a=![]() c2+
c2+![]() b(ab),
b(ab),
化简得:ab+a2=c2+abb2,
∴a2+b2=c2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目