题目内容
已知四边形ABCD，有
①AB∥CD；②AB=CD；③BC∥AD；④BC="AD." 从这四个条件中任选两个, 能使四边形ABCD成为平行四边形的选法种数，共有( )
A．3种 B．4种 C．5种 D．6种
①AB∥CD；②AB=CD；③BC∥AD；④BC="AD." 从这四个条件中任选两个, 能使四边形ABCD成为平行四边形的选法种数，共有( )
A．3种 B．4种 C．5种 D．6种
B
根据平行四边形的判定方法，①与③，②与④，①与②，④与③均可得证四边形是平行四边形
证明：①、③：根据两组对边分别平行的四边形为平行四边形即可证出；
②、④：根据两组对边分别相等的四边形为平行四边形即可证出；
①、②：根据一组对边平行且相等的四边形为平行四边形即可证出；
④、③：根据一组对边平行且相等的四边形为平行四边形即可证出．
故答案选B.
点评：平行四边形的五种判定方法分别是：（1）两组对边分别平行的四边形是平行四边形；（2）两组对边分别相等的四边形是平行四边形；（3）一组对边平行且相等的四边形是平行四边形；（4）两组对角分别相等的四边形是平行四边形；（5）对角线互相平分的四边形是平行四边形．
证明：①、③：根据两组对边分别平行的四边形为平行四边形即可证出；
②、④：根据两组对边分别相等的四边形为平行四边形即可证出；
①、②：根据一组对边平行且相等的四边形为平行四边形即可证出；
④、③：根据一组对边平行且相等的四边形为平行四边形即可证出．
故答案选B.
点评：平行四边形的五种判定方法分别是：（1）两组对边分别平行的四边形是平行四边形；（2）两组对边分别相等的四边形是平行四边形；（3）一组对边平行且相等的四边形是平行四边形；（4）两组对角分别相等的四边形是平行四边形；（5）对角线互相平分的四边形是平行四边形．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
平分
；
，求
的面积.
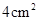，则梯形ABCD的面积为 cm2．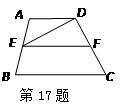
被两条与边平行的线段
分割成四个小矩形，
与
交于点
．
，证明：
；
，证明：
；
的周长为1，求矩形
的面积．
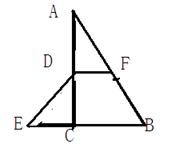
，D、F分别是AB、AC的中点，延长BC到点E，使
