题目内容
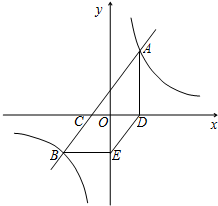
如图,已知直线AB与x轴交于点C,与双曲线
y=交于A(3,
)、B(-5,a)两点.AD⊥x轴于点D,BE∥x轴且与y轴交于点E.
(1)求点B的坐标及直线AB的解析式;
(2)判断四边形CBED的形状,并说明理由.
分析:(1)根据反比例函数图象上点的坐标特征,将点A代入双曲线方程求得k值,即利用待定系数法求得双曲线方程;然后将B点代入其中,从而求得a值;设直线AB的解析式为y=mx+n,将A、B两点的坐标代入,利用待定系数法解答;
(2)由点C、D的坐标、已知条件“BE∥x轴”及两点间的距离公式求得,CD=5,BE=5,且BE∥CD,从而可以证明四边形CBED是平行四边形;然后在Rt△OED中根据勾股定理求得ED=5,所以ED=CD,从而证明四边形CBED是菱形.
解答:解:(1)∵双曲线
y=过A(3,
),
∴k=20.
把B(-5,a)代入
y=,得
a=-4.
∴点B的坐标是(-5,-4).(2分)
设直线AB的解析式为y=mx+n,
将A(3,
)、B(-5,-4)代入,得
,
解得:
,
∴直线AB的解析式为:
y=x+;(4分)
(2)四边形CBED是菱形.理由如下:(5分)
∵直线AB的解析式为:
y=x+,
∴当y=0时,x=-2,
∴点C的坐标是(-2,0);
∵点D在x轴上,AD⊥x轴,A(3,
),
∴点D的坐标是(3,0),
∵BE∥x轴,
∴点E的坐标是(0,-4).
而CD=5,BE=5,且BE∥CD.
∴四边形CBED是平行四边形.(6分)
在Rt△OED中,ED
2=OE
2+OD
2,
∴ED=
=
=
=5,
∴ED=CD.
∴平行四边形CBED是菱形.(8分)
点评:本题考查了反比例函数综合题.解答此题时,利用了反比例函数图象上点的坐标特征.
练习册系列答案
相关题目
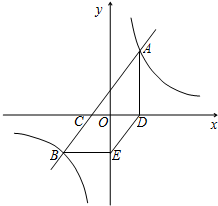 如图,已知直线AB与x轴交于点C,与双曲线y=
如图,已知直线AB与x轴交于点C,与双曲线y=
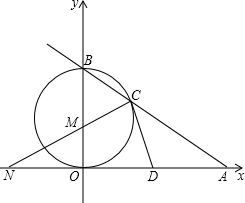 方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM.
方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM.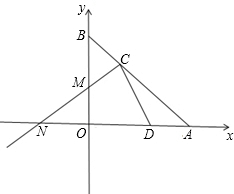 如图,已知直线AB与x轴、y轴分别交于A和B,OA=4,且OA、OB长是关于x的方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM并延长交x轴于N.
如图,已知直线AB与x轴、y轴分别交于A和B,OA=4,且OA、OB长是关于x的方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM并延长交x轴于N. 26、如图,已知直线AB与CD相交于点O,OB平分∠EOD,∠1+∠2=90°,
26、如图,已知直线AB与CD相交于点O,OB平分∠EOD,∠1+∠2=90°, A=3,点C的横坐标为-3,tan∠BAO=
A=3,点C的横坐标为-3,tan∠BAO= 如图,已知直线AB与CD相交于点O,OE⊥CD,OF平分∠BOE,若∠AOC=∠EOF,
如图,已知直线AB与CD相交于点O,OE⊥CD,OF平分∠BOE,若∠AOC=∠EOF,