题目内容
如图,已知直线AB与x轴、y轴分别交于A和B,OA=4,且OA、OB长是关于x的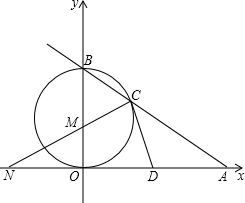 方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM.
方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM.(1)求⊙M的半径.
(2)若D为OA的中点,求证:CD是⊙M的切线.
分析:(1)由OA、OB长是关于x的方程x2-mx+12=0的两实根,得OA•OB=12,而OA=4,所以OB=3,又由于OB为⊙M的直径,即可得到⊙M的半径.
(2)连MD,OC,由OB为⊙M的直径,得∠OCB=90°,则∠OCD=90°,由于D为OA的中点,所以CD=
OA=OD,因此可证明△MCD≌△MOD,所以∠MCD=∠MOD=90°,即CD是⊙M的切线.
(2)连MD,OC,由OB为⊙M的直径,得∠OCB=90°,则∠OCD=90°,由于D为OA的中点,所以CD=
| 1 |
| 2 |
解答:(1)解:∵OA、OB长是关于x的方程x2-mx+12=0的两实根,
∴OA•OB=12,而OA=4,
∴OB=3,
又∵OB为⊙M的直径,
∴⊙M的半径为
.
(2)证明:连MD,OC,如图,
∵OB为⊙M的直径,
∴∠OCB=90°,
又∵D为OA的中点,
∴CD=
OA=OD,
而MC=MO,MD公共,
∴△MCD≌△MOD,
∴∠MCD=∠MOD=90°,
所以CD是⊙M的切线.
∴OA•OB=12,而OA=4,
∴OB=3,
又∵OB为⊙M的直径,
∴⊙M的半径为
| 3 |
| 2 |
(2)证明:连MD,OC,如图,

∵OB为⊙M的直径,
∴∠OCB=90°,
又∵D为OA的中点,
∴CD=
| 1 |
| 2 |
而MC=MO,MD公共,
∴△MCD≌△MOD,
∴∠MCD=∠MOD=90°,
所以CD是⊙M的切线.
点评:本题考查了圆的切线的判定方法.经过半径的外端点与半径垂直的直线是圆的切线.当已知直线过圆上一点,要证明它是圆的切线,则要连接圆心和这个点,证明这个连线与已知直线垂直即可;当没告诉直线过圆上一点,要证明它是圆的切线,则要过圆心作直线的垂线,证明垂线段等于圆的半径.同时考查了直径所对的圆周角为90度,直角三角形斜边上的中线等于斜边的一半以及三角形全等的判定和性质.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
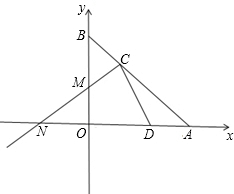 如图,已知直线AB与x轴、y轴分别交于A和B,OA=4,且OA、OB长是关于x的方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM并延长交x轴于N.
如图,已知直线AB与x轴、y轴分别交于A和B,OA=4,且OA、OB长是关于x的方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM并延长交x轴于N. 26、如图,已知直线AB与CD相交于点O,OB平分∠EOD,∠1+∠2=90°,
26、如图,已知直线AB与CD相交于点O,OB平分∠EOD,∠1+∠2=90°, A=3,点C的横坐标为-3,tan∠BAO=
A=3,点C的横坐标为-3,tan∠BAO= 如图,已知直线AB与CD相交于点O,OE⊥CD,OF平分∠BOE,若∠AOC=∠EOF,
如图,已知直线AB与CD相交于点O,OE⊥CD,OF平分∠BOE,若∠AOC=∠EOF,