题目内容
 如图,已知直线AB与CD相交于点O,OE⊥CD,OF平分∠BOE,若∠AOC=∠EOF,
如图,已知直线AB与CD相交于点O,OE⊥CD,OF平分∠BOE,若∠AOC=∠EOF,(1)求∠AOC的度数;
(2)写出∠EOF的余角和补角.
分析:(1)由角平分线的性质得出∠EOF=∠BOF,根据等量关系可得∠AOC=∠BOD=∠EOF,依此可得∠AOC的度数;
(2)根据余角和补角的定义、性质求得答案即可.
(2)根据余角和补角的定义、性质求得答案即可.
解答:解:(1)∵OE⊥CD,
∴∠COE=∠DOE=90°,
∵OF平分∠BOE,
∴∠EOF=∠BOF,
∵∠AOC=∠BOD=∠EOF,
∴∠BOD=∠BOF=∠EOF=30°,(3分)
∴∠AOC=30°,(3分)
(2)∵∠EOF=30°,
∴它的余角为60°,即:∠BOE、∠DOF;
∴它的补角为150°,即:∠BOC、∠AOF、∠AOD.
∴∠COE=∠DOE=90°,
∵OF平分∠BOE,
∴∠EOF=∠BOF,
∵∠AOC=∠BOD=∠EOF,
∴∠BOD=∠BOF=∠EOF=30°,(3分)
∴∠AOC=30°,(3分)
(2)∵∠EOF=30°,
∴它的余角为60°,即:∠BOE、∠DOF;
∴它的补角为150°,即:∠BOC、∠AOF、∠AOD.
点评:本题考查了余角和补角的定义以及性质、角平分线的性质,若两个角的和为90°,则这两个角互余;若两个角的和等于180°,则这两个角互补.

练习册系列答案
相关题目
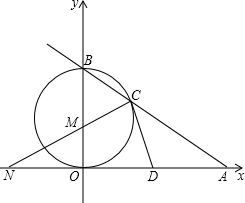 方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM.
方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM.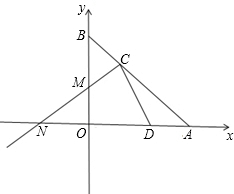 如图,已知直线AB与x轴、y轴分别交于A和B,OA=4,且OA、OB长是关于x的方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM并延长交x轴于N.
如图,已知直线AB与x轴、y轴分别交于A和B,OA=4,且OA、OB长是关于x的方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM并延长交x轴于N. 26、如图,已知直线AB与CD相交于点O,OB平分∠EOD,∠1+∠2=90°,
26、如图,已知直线AB与CD相交于点O,OB平分∠EOD,∠1+∠2=90°, A=3,点C的横坐标为-3,tan∠BAO=
A=3,点C的横坐标为-3,tan∠BAO=