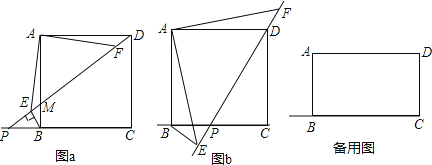
��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=![]() ��������y=
��������y=![]() ����A��B���㣬�ҵ�A��x���ϣ���B�ĺ�����Ϊ-4����PΪֱ��AB�Ϸ�����������һ���㣨�����A��B�غϣ�������P��x��Ĵ��߽�ֱ��AB�ڵ�Q��PH��AB��H��
����A��B���㣬�ҵ�A��x���ϣ���B�ĺ�����Ϊ-4����PΪֱ��AB�Ϸ�����������һ���㣨�����A��B�غϣ�������P��x��Ĵ��߽�ֱ��AB�ڵ�Q��PH��AB��H��
��1����b��ֵ��sin��PQH��ֵ��
��2�����P�ĺ�����Ϊt���ú�t�Ĵ���ʽ��ʾ��P��ֱ��AB�ľ���PH�ij��������PH֮�������ֵ�Լ���ʱt��ֵ��
��3������PB�����߶�PQ����PBH�ֳɳ���PQB����PQH�������ȣ����ʱ��P�����꣮
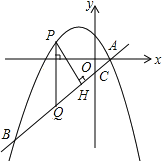
���𰸡���1��b=-1��![]() ����2��
����2��![]() ����t=-1ʱ��PH�����ֵΪ
����t=-1ʱ��PH�����ֵΪ![]() ����3��P��-3��0����
����3��P��-3��0����
��������
��1����y=0�������A�����꣬Ȼ��ѵ�A���������ֱ�߽���ʽ�������B��ֵ��Ȼ����ݵ�A�͵�C�����꣬���OA��OC�ij��ȣ����ݹ��ɶ������AC�ij��ȣ�����PQ��OC���ɵá�PQH=��OCA��Ȼ�����sin��PQH��ֵ��
��2�������P�͵�Q�����꣬�������Ǻ��������PH�ĺ�����ϵʽ�����������ֵ�ķ�����⼴�ɣ�
��3����BD��PQ��PQ���ӳ����ڵ�D����S��PQB=S��PQH���ó�BQ=QH���������Ǻ������QH��BQ�Ĺ�ϵʽ��������ȵĹ�ϵ���t�����ɵó���P�����꣮
�⣺��1����y=0�ã�![]() ������x2+x-6=0�����x1=-3��x2=2��
������x2+x-6=0�����x1=-3��x2=2��
��A��2��0����
��A��2��0����ֱ��![]() �ϣ�
�ϣ�
��1+b=0�����b=-1��
��OC=1��OA=2��
![]() ��
��
��PQ��OC��
���PQH=��OCA��
![]() ��
��
��2��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
�൱t=-1ʱ��PH�����ֵΪ![]() ��
��
��3����ͼ����BD��PQ��PQ���ӳ����ڵ�D�����P�ĺ�����Ϊt��
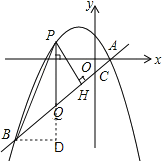
��S��PQB=S��PQH��
��BQ=QH��
��RT��PHQ��
![]() ��
��
![]() ��
��
![]() ��
��
��RT��BDQ��
�ߡ�BQD=��PQH��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
��t2+7t+12=0��
��t1=-3��t2=-4����ȥ����
��P��-3��0����

 ��ҵ����ϵ�д�
��ҵ����ϵ�д�