题目内容
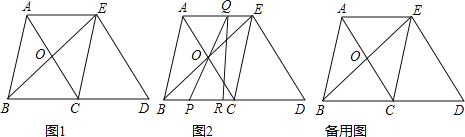
【题目】如图,已知∠AOB=60°,在∠AOB的平分线OM上有一点C,将一个120°角的顶点与点C重合,它的两条边分别与直线OA、OB相交于点D、E.
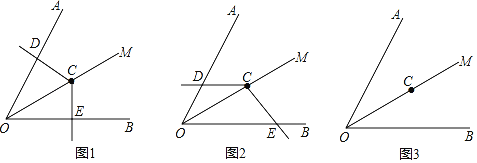
(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OE+OD与OC的数量关系,并说明理由;
(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;
(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?请在图3中画出图形,若成立,请给于证明;若不成立,线段OD、OE与OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
【答案】(1)![]() ;(2)(1)中结论仍然成立,见解析;(3)(1)中结论不成立,
;(2)(1)中结论仍然成立,见解析;(3)(1)中结论不成立, ![]() ,见解析.
,见解析.
【解析】
(1)先判断出∠OCE=60°,再利用特殊角的三角函数得出OD![]() OC,同OE
OC,同OE![]() OC,即可得出结论;
OC,即可得出结论;
(2)同(1)的方法得OF+OG![]() OC,再判断出△CFD≌△CGE,得出DF=EG,最后等量代换即可得出结论;
OC,再判断出△CFD≌△CGE,得出DF=EG,最后等量代换即可得出结论;
(3)同(2)的方法即可得出结论.
(1)∵OM是∠AOB的角平分线,
∴∠AOC=∠BOC![]() ∠AOB=30°.
∠AOB=30°.
∵CD⊥OA,∴∠ODC=90°,
∴∠OCD=60°,
∴∠OCE=∠DCE﹣∠OCD=60°.
在Rt△OCD中,OD=OCcos30°![]() OC,
OC,
同理:OE![]() OC,
OC,
∴OD+OE![]() OC;
OC;
(2)(1)中结论仍然成立,理由如下:
过点C作CF⊥OA于F,CG⊥OB于G,
∴∠OFC=∠OGC=90°.
∵∠AOB=60°,
∴∠FCG=120°,
同(1)的方法得:OF![]() OC,OG
OC,OG![]() OC,
OC,
∴OF+OG![]() OC.
OC.
∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,
∴CF=CG.
∵∠DCE=120°,∠FCG=120°,
∴∠DCF=∠ECG,
∴△CFD≌△CGE,
∴DF=EG,
∴OF=OD+DF=OD+EG,OG=OE﹣EG,
∴OF+OG=OD+EG+OE﹣EG=OD+OE,
∴OD+OE![]() OC;
OC;
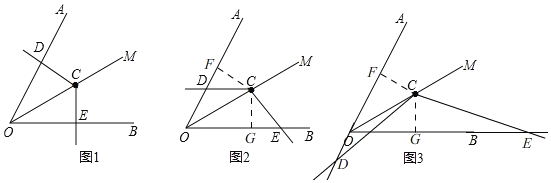
(3)(1)中结论不成立,结论为:OE﹣OD![]() OC,理由如下:
OC,理由如下:
过点C作CF⊥OA于F,CG⊥OB于G,
∴∠OFC=∠OGC=90°.
∵∠AOB=60°,
∴∠FCG=120°,
同(1)的方法得:OF![]() OC,OG
OC,OG![]() OC,
OC,
∴OF+OG![]() OC.
OC.
∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,
∴CF=CG.
∵∠DCE=120°,∠FCG=120°,
∴∠DCF=∠ECG,
∴△CFD≌△CGE,
∴DF=EG,
∴OF=DF﹣OD=EG﹣OD,OG=OE﹣EG,
∴OF+OG=EG﹣OD+OE﹣EG=OE﹣OD,
∴OE﹣OD![]() OC.
OC.