题目内容
【题目】已知关于x的方程mx2+（4-3m）x+2m-8=0（m＞0）．
（1）求证：方程有两个不相等的实数根；
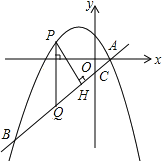
（2）设方程的两个根分别为x1、x2（x1＜x2），若n=x2-x1
m，且点B（m，n）在x轴上，求m的值．
【答案】（1）见解析；（2）m=4．
【解析】
（1）首先得到△=（4-3m）2-4m（2m-8）=m2+8m+16=（m+4）2然后根据m＞0得到（m+4）2＞0从而得到△＞0，最后证得方程有两个不相等的实数根；
（2）利用根与系数的关系得出关于m的方程求得答案即可．
解：（1）∵△=（4-3m）2-4m（2m-8），
=m2+8m+16
=（m+4）2
又∵m＞0
∴（m+4）2＞0
即△＞0
∴方程有两个不相等的实数根；
（2）∵方程的两个根分别为x1、x2（x1＜x2），
，
，且点B（m，n）在x轴上，
，
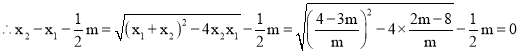解得：m=-2，m=4，
∵m＞0，
∴m=4．
练习册系列答案
相关题目
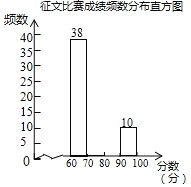
【题目】今年我区作为全国作文教学改革试验区，举办了中小学生现场作文大赛，全区七、八年级的学生参加了中学组的比赛，大赛组委会对参赛获奖作品的成绩进行统计，每篇获奖作品成绩为m分（60≤m≤100）绘制了如下两幅数据信息不完整的统计图表．
获奖作品成绩频数分布表
分数段 | 频数 | 频率 |
60≤x＜70 | 38 | 0.38 |
70≤x＜80 | a | 0.32 |
80≤x＜90 | b | |
90≤x＜100 | 10 | |
合计 | 1 |
请根据以上信息，解决下列问题：
（1）获奖作品成绩频数分布表中a＝ ，b＝ ；
（2）把获奖作品成绩频数分布直方图缺失的信息补全；
（3）某校八年级二班有两名男同学和两名女同学在这次大赛中获奖，并且其中两名同学获得了大赛一等奖，请用列表或画树状图法求出恰好一男一女获得一等奖的概率．
