题目内容
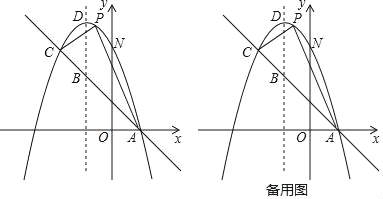
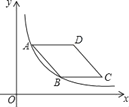
【题目】如图,正方形ABCD,点P在射线CB上运动(不包含点B、C),连接DP,交AB于点M,作BE⊥DP于点E,连接AE,作∠FAD=∠EAB,FA交DP于点F.
(1)如图a,当点P在CB的延长线上时,
①求证:DF=BE;
②请判断DE、BE、AE之间的数量关系并证明;
(2)如图b,当点P在线段BC上时,DE、BE、AE之间有怎样的数量关系?请直接写出答案,不必证明;
(3)如果将已知中的正方形ABCD换成矩形ABCD,且AD:AB=![]() :1,其他条件不变,当点P在射线CB上时,DE、BE、AE之间又有怎样的数量关系?请直接写出答案,不必证明.
:1,其他条件不变,当点P在射线CB上时,DE、BE、AE之间又有怎样的数量关系?请直接写出答案,不必证明.
【答案】(1)详见解析;②DE=BE+![]() AE,理由详见解析;(2)DE=
AE,理由详见解析;(2)DE=![]() AE﹣BE;(3)DE=2AE+
AE﹣BE;(3)DE=2AE+![]() BE或DE=2AE﹣
BE或DE=2AE﹣![]() BE.
BE.
【解析】
(1)①由正方形的性质得到AD=AB,∠BAD=90°,判断出△ABE≌△ADF,即可;②由①得到△ABE≌△ADF,并且判断出△EAF为直角三角形,用勾股定理即可;
(2)先由正方形的性质和已知条件判断出△ABE≌△ADF,再用判断出△EAF为直角三角形,用勾股定理即可;
(3)分两种情况讨论,先由正方形的性质和已知条件判断出△ABE∽△ADF,AF=![]() AE,DF=
AE,DF=![]() BE,再判断出△EAF为直角三角形,用勾股定理结合图形可得结论.
BE,再判断出△EAF为直角三角形,用勾股定理结合图形可得结论.
证明:(1)①正方形ABCD中,AD=AB,∠ADM+∠AMD=90°
∵BE⊥DP,
∴∠EBM+∠BME=90°,
∵∠AMD=∠BME,
∴∠EBM=∠ADM,
在△ABE和△ADF中,
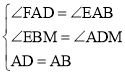 ,
,
∴△ABE≌△ADF,
∴DF=BE;
②DE=BE+![]() AE,
AE,
理由:由(1)有△ABE≌△ADF,
∴AE=AF,∠BAE=∠DAF,
∴∠BAE+∠FAM=∠DAF+∠FAM,
∴∠EAF=∠BAD=90°,
∴EF=![]() AE,
AE,
∵DE=DF+EF,
∴DE=BE+![]() AE;
AE;
(2)DE=![]() AE﹣BE;
AE﹣BE;
理由:正方形ABCD中,AD=AB,∠BAD=∠BAE+∠DAE=90°,
∵∠FAD=∠EAB,
∴∠EAF=∠BAD=90°,
∴∠AFE+∠AEF=90°
∵BE⊥DP,
∴∠BEA+∠AEF=90°,
∴∠BEA=∠AFE,
∵∠FAD=∠EAB,AD=AB
∴△ABE≌△ADF,
∴AE=AF,BE=DF
∵∠EAF=90°
∴EF=![]() AE,
AE,
∵EF=DF+DE=![]() AE,
AE,
∴DE=![]() AE﹣DF=
AE﹣DF=![]() AE﹣BE;
AE﹣BE;
(3)DE=2AE+![]() BE或DE=2AE﹣
BE或DE=2AE﹣![]() BE.
BE.
①如图1所示时,
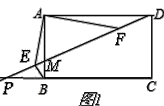
正方形ABCD中,∠ADM+∠AMD=90°
∵BE⊥DP,
∴∠EBM+∠BME=90°,
∵∠AMD=∠BME,
∴∠EBM=∠ADM,
∵∠FAD=∠EAB
∴△ABE∽△ADF,
∴![]() ,
,
∵AD:AB=![]() :1,
:1,
∴![]() ,
,
∴AF=![]() AE,DF=
AE,DF=![]() BE
BE
∵∠FAD=∠EAB
∴∠EAF=∠EAB+∠BAF=∠FAD+∠BAF=∠BAD=90°,
∴EF=![]() =2AE=DE﹣DF=DE﹣
=2AE=DE﹣DF=DE﹣![]() BE,
BE,
即:DE=2AE+![]() BE;
BE;
②如图2所示,
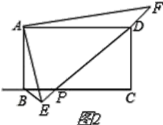
∵∠DAF=∠BAE,
∴∠EAF=∠BAD=90°,
∵∠DAF=∠BAE,
∴△BAE∽△DAF,
∴![]() ,
,
∵AD:AB=![]() :1,
:1,
∴![]() ,
,
∴AF=![]() AE,DF=
AE,DF=![]() BE,
BE,
∵∠EAF=90°,
根据勾股定理得,EF=![]() =2AE=DE+DF=DE+
=2AE=DE+DF=DE+![]() BE,
BE,
∴DE=2AE﹣![]() BE.
BE.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案【题目】某一天,水果经营户老张用1600元从水果批发市场批发猕猴桃和芒果共50千克,后再到水果市场去卖,已知猕猴桃和芒果当天的批发价和零售价如表所示:
品名 | 猕猴桃 | 芒果 |
批发价 | 20 | 40 |
零售价 | 26 | 50 |
![]() 他购进的猕猴桃和芒果各多少千克?
他购进的猕猴桃和芒果各多少千克?
![]() 如果猕猴桃和芒果全部卖完,他能赚多少钱?
如果猕猴桃和芒果全部卖完,他能赚多少钱?