Question

【题目】甲、乙、丙三位同学在操场上互相传球，假设他们相互间传球是等可能的，并且由甲首先开始传球．
（1）经过2次传球后，球仍回到甲手中的概率是；
（2）请用列举法（画树状图或列表）求经过3次传球后，球仍回到甲手中的概率；
（3）猜想并直接写出结论：经过n次传球后，球传到甲、乙这两位同学手中的概率：P（球传到甲手中）和P（球传到乙手中）的大小关系．

Answer 1

【答案】
（1）解：画树状图为：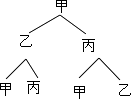
共有4种等可能的结果数，其中球仍回到甲手中的结果数为2，
所以球仍回到甲手中的概率= = ；
故答案为
（2）解：画树状图为：

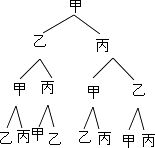
共有8种等可能的结果数，其中球仍回到甲手中的结果数为2，

所以球仍回到甲手中的概率= =

（3）解：当n为偶数时，P（球传到甲手中）＞P（球传到乙手中）的大小关系；

当n为奇数时，P（球传到甲手中）＜P（球传到乙手中）的大小关系

【解析】（1）画树状图展示所有4种等可能的结果数，再找出球仍回到甲手中的结果数，然后根据概率公式求解；（2）画树状图展示所有8种等可能的结果数，再找出球仍回到甲手中的结果数，然后根据概率公式求解；（3）利用（1）、（2）的结论讨论：当n为偶数时，P（球传到甲手中）＞P（球传到乙手中）的大小关系；当n为奇数时，P（球传到甲手中）＜P（球传到乙手中）的大小关系．
【考点精析】根据题目的已知条件，利用列表法与树状图法的相关知识可以得到问题的答案，需要掌握当一次试验要设计三个或更多的因素时，用列表法就不方便了，为了不重不漏地列出所有可能的结果，通常采用树状图法求概率．