��Ŀ����
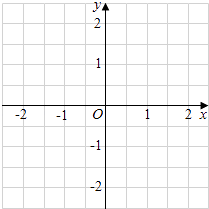
����Ŀ����ͼ1��ʾ����֪y= ![]() ��x��0��ͼ����һ��P��PA��x���ڵ�A��a��0������B����Ϊ��0��b����b��0��������M��y����������B���Ϸ��ĵ㣬����N������AP�ϣ�����B��AB�Ĵ��ߣ�������AP�ڵ�D����ֱ��MN�ڵ�Q����AQ��ȡAQ���е�ΪC��
��x��0��ͼ����һ��P��PA��x���ڵ�A��a��0������B����Ϊ��0��b����b��0��������M��y����������B���Ϸ��ĵ㣬����N������AP�ϣ�����B��AB�Ĵ��ߣ�������AP�ڵ�D����ֱ��MN�ڵ�Q����AQ��ȡAQ���е�ΪC��
��1����ͼ2������BP�����PAB�������
��2������Q���߶�BD��ʱ�����ı���BQNC�����Σ����Ϊ2 ![]() �����ʱP������ꣻ
�����ʱP������ꣻ
��3������Q������BD��ʱ����a=3��b=1�����Ե�B��C��N��QΪ������ı�����ƽ���ı��Σ������ƽ���ı��ε��ܳ���
���𰸡�
��1��
�⣺��ͼ2������OP��
S��PAB=S��PAO= ![]() xy=
xy= ![]() ��6=3
��6=3

��2��
�⣺��ͼ3��

���ı���BQNC�����Σ�
��BQ=BC=NQ����BQC=��NQC��
��AB��BQ��C��AQ���е㣬
��BC=CQ= ![]() AQ��
AQ��
���BQC=60�㣬��BAQ=30�㣬
�ڡ�ABQ�͡�ANQ�У�
 ��
��
���ABQ�ա�ANQ��SAS����
���BAQ=��NAQ=30�㣬
���BAO=30�㣬
��S����BQNC=2 ![]() =
= ![]() ��CQ��BN��
��CQ��BN��
��CQ=2t=BQ����BN=2����2t�� ![]() ��=2
��=2 ![]() t��
t��
��t=1
��BQ=2��
����Rt��AQB�У���BAQ=30�㣬
��AB= ![]() BQ=2
BQ=2 ![]() ��
��
�ߡ�BAO=30��
��OA= ![]() AB=3��
AB=3��
�֡�P���ڷ���������y= ![]() ��ͼ���ϣ�
��ͼ���ϣ�
��P��������3��2��
��3��
�⣺��OB=1��OA=3��
��AB= ![]() ��
��
�á�AOB�ס�DBA��
�� ![]() ��
��
��BD=3 ![]() ��
��
����ͼ3������Q���߶�BD�ϣ�

��AB��BD��CΪAQ���е㣬
��BC= ![]() AQ��
AQ��
���ı���BQNC��ƽ���ı��Σ�
��QN=BC��CN=BQ��CN��BD��
�� ![]() =
= ![]() ��
��
��BQ=CN= ![]() BD=
BD= ![]() ��
��
��AQ= ![]() =2
=2 ![]() ��
��
��C�ı���BQNC=2 ![]() +2
+2 ![]() ��
��
����ͼ4������Q������BD���ӳ����ϣ�

��AB��BD��CΪAQ���е㣬
��BC=CQ= ![]() AQ��
AQ��
��ƽ���ı���BNQC�����Σ�BN=CQ��BN��CQ��
���BND�ס�QAD
�� ![]() =
= ![]() ��
��
��BQ=3BD=9 ![]() ��
��
��AQ= ![]() =
= ![]() =2
=2 ![]() ��
��
��C�ı���BNQC=2AQ=4 ![]() ��
��
����������1������ͬ�ȸߵ����������ε������ȼ��������PAB���������2�����������BQC=60�㣬��BAQ=30�㣬Ȼ��֤����ABQ�ա�ANQ�����������BAO=30�㣬��S�ı���BQNC=2 ![]() �����OA=3������P�������������3��������������ۣ�����Q���߶�BD�ϣ���������������AQ�ij�����������ı��ε��ܳ�������Q���߶�BD���ӳ����ϣ���Ȼ��������������AQ�ij����ٽ�һ������ı��ε��ܳ���
�����OA=3������P�������������3��������������ۣ�����Q���߶�BD�ϣ���������������AQ�ij�����������ı��ε��ܳ�������Q���߶�BD���ӳ����ϣ���Ȼ��������������AQ�ij����ٽ�һ������ı��ε��ܳ���
�����㾫����������Ҫ�����˷�����������ͼ��ͷ��������������ʵ����֪ʶ�㣬��Ҫ���շ�����������ͼ������˫���ߣ�������������ͼ�������Գ�ͼ���������ĶԳ�ͼ�Σ��������Գ��ֱ��y=x�� y=-x���Գ������ǣ�ԭ�㣻����:��k��0ʱ˫���ߵ���֧�ֱ�λ�ڵ�һ���������ޣ���ÿ��������yֵ��xֵ���������С�� ��k��0ʱ˫���ߵ���֧�ֱ�λ�ڵڶ����������ޣ���ÿ��������yֵ��xֵ����������������ȷ�����⣮

����Ŀ��LED�ƾ��л������ܡ�Ͷ�䷶Χ����Ƶ����ʹ�������ϳ����ص㣬���ճ������У����Ǹ�������LED�Ƶ�ʹ�ã�ijУ��ѧ��ȤС��Ϊ�˽�LED��������ͨ�׳���ݵ�����������������г����飺ij�̳�����һ��30�ߵ�LED���ݺ���ͨ�׳���ݽ������ۣ�������������±���
LED���� | ��ͨ�׳���� | |
���ۣ�Ԫ�� | 45 | 25 |
��ۣ�Ԫ�� | 60 | 30 |

��1�����̳�������LED��������ͨ�׳���ݹ�300����LED���ݰ���۽������ۣ�����ͨ�׳���ݴ�������ۣ����������������ݺ���Ի���3200Ԫ������̳�����LED��������ͨ�׳���ݵ������ֱ�Ϊ���ٸ���
��2�����ڴ����ڼ��������ܿ콫���ֵ��������꣬�����̳��ƻ��ٴι������ֵ���120�����ڲ����۵�����£�������ν�������������������ʱ��������Ҳ����������۵�30%���������ʱ�������ݵ�������Ϊ����Ԫ��
����Ŀ��Ϊӭ���й�ɭ���ᣬij�̼Ҽƻ��ӳ��Ҳɹ�A��B���ֲ�Ʒ��20������Ʒ�IJɹ����ۣ�Ԫ/�����Dzɹ�������������һ�κ������±��ṩ�˲��ֲɹ����ݣ�
�ɹ����������� | 1 | 2 | �� |
A��Ʒ���ۣ�Ԫ/���� | 1480 | 1460 | �� |
B��Ʒ���ۣ�Ԫ/���� | 1290 | 1280 | �� |
��1����A��Ʒ�IJɹ�����Ϊx���������ɹ�����Ϊy1��Ԫ/��������y1��x�Ĺ�ϵʽ��
��2�����̼��볧��Э�̣��ɹ�A��Ʒ������������B��Ʒ������ ![]() ����A��Ʒ�ɹ����۲�����1200Ԫ������̼ҹ��м��ֽ���������
����A��Ʒ�ɹ����۲�����1200Ԫ������̼ҹ��м��ֽ���������
��3�����̼ҷֱ���1760Ԫ/����1700Ԫ/�������۵����۳�A��B���ֲ�Ʒ����ȫ�����꣬�ڣ�2���������£���ɹ�A�ֲ�Ʒ���ټ�ʱ������������������