Question

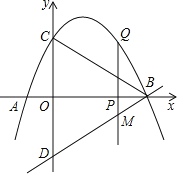
【题目】如图，在平面直角坐标系中，过原点O及A（8，0）、C（0，6）作矩形OABC，连接AC，一个直角三角形PDE的直角顶点P始终在对角线AC上运动（不与A、C重合），且保持一边PD始终经过矩形顶点B，PE交x轴于点Q

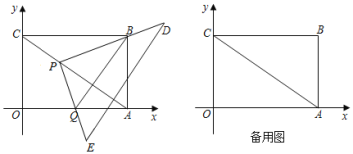
（1）＝______；

（2）在点P从点C运动到点A的过程中，的值是否发生变化？如果变化，请求出其变化范围，如果不变，请说明理由，并求出其值；

（3）若将△QAB沿直线BQ折叠后，点A与点P重合，则PC的长为_____．

Answer 1

【答案】（1）；（2）的值不发生变化，＝，理由见解析；（3）2.8．

【解析】

（1）根据A、C两点坐标可得OA、OC的长，根据矩形的性质可得AB=OC、BC=OA，即可得答案；（2）由∠OAB＝∠BPQ=90°，根据四边形内角和可得∠AOB+∠BPQ＝180°，可得A、B、P、Q四点共圆，根据圆周角定理可得∠PQB＝∠PAB，即可证明△PBQ∽△BCA，根据相似三角形的性质可得＝＝，即可得答案；（3）设BQ交AP于M，利用勾股定理可得AC=10，根据折叠性质可得BQ⊥AP，PM＝AM，即可证明△ABM∽△ACB，根据相似三角形的性质可求出AM的长，进而求出PC的长即可.

（1）∵A（8，0）、C（0，6），

∴OA＝8，OC＝6，

∵四边形OABC是矩形，

∴∠ABC＝∠OAB＝90°，BC＝OA＝8，AB＝OC＝6，

∴＝＝ ，

故答案为：

（2）的值不发生变化，＝，理由如下：

∵∠OAB＝∠BPQ＝90°，

∴∠PQA+∠ABP＝180°，

∴A、B、P、Q四点共圆，

∴∠PQB＝∠PAB，

∵∠ABC＝∠BPQ＝90°，

∴△PBQ∽△BCA，

∴＝＝.

∴的值不发生变化，＝.

（3）设BQ交AP于M，如图所示：

在Rt△ABC中，由勾股定理得：AC＝＝＝10，

由折叠的性质得：BQ⊥AP，PM＝AM，

∴∠AMB＝90°＝∠ABC，

∵∠BAM＝∠CAB，

∴△ABM∽△ACB，

∴＝，即＝，

解得：AM＝3.6，

∴PA＝2AM＝7.2，

∴PC＝AC﹣PA＝10﹣7.2＝2.8，

故答案为：2.8