题目内容
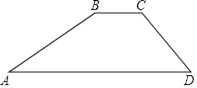
【题目】如图,一水库大坝的横断面为梯形ABCD,坝顶宽6米,坝高10米,斜坡AB的坡度i1=1:3,斜坡CD的坡度i2=1:1.
(1)求斜坡AB的长(结果保留根号);
(2)求坝底AD的长度;
(3)求斜坡CD的坡角α.
【答案】(1)斜坡AB的长为10![]() m;(2)坝底AD的长度为46m;(3)α=45°
m;(2)坝底AD的长度为46m;(3)α=45°
【解析】
(1)根据坡度的概念求出AE的长,根据勾股定理求出AB的长;
(2)分别得出DF,EF的长,进而得出答案;
(3)根据坡度是坡角的正切值计算即可.
(1)过点B,作BE⊥AD于点E,
∵坝高10米,斜坡AB的坡度i1=1:3,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:AE=30m,
则AB=![]() =10
=10![]() (m),
(m),
答:斜坡AB的长为10![]() m;
m;
(2)过点C作CF⊥AD于点F,
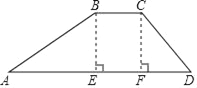
∵斜坡CD的坡度i2=1:1,坝高10米,
∴BC=EF=6m,CF=FD=10m,
∴AD=AE+EF+FD=30+6+10=46(m),
答:坝底AD的长度为46m;
(3)∵斜坡CD的坡度i2=1:1,
∴斜坡CD的坡角α为:tanα=1,
则α=45°

练习册系列答案
相关题目