题目内容
【题目】如图,抛物线y=ax2+2x与x轴相交于点B,其对称轴为x=3.
(1)求直线AB的解析式;
(2)过点O作直线l,使l∥AB,点P是l上一动点,设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为t,当0<S≤18时,求t的取值范围;
(3)在(2)的条件下,当t取最大值时,抛物线上是否存在点Q,使△OPQ为直角三角形且OP为直角边,若存在,求出点Q的坐标;若不存在,说明理由.
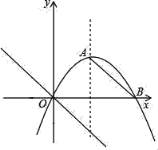
【答案】(1)y=﹣x+6;(2)﹣3≤t<0或0<t≤3;(3)存在.点Q的坐标为(3,3)或(6,0)或(﹣3,﹣9).
【解析】
(1)利用抛物线的对称性得到点B坐标为(6,0),再把B点坐标代入y=ax2+2x中求出a得到抛物线解析式;接着把一般式配成顶点式得到A点坐标,然后利用待定系数法求直线AB的解析式;
(2)易得直线解析式为y=-x,则可设P点坐标为(t,-t),讨论:当点P在第四象限时(t>0),利用三角形面积公式可得到S=S△AOB+S△POB=9+3t,再利用S的范围可得到t的范围;当点P在第二象限时(t<0),作PM⊥x轴于M,设对称轴与x轴交点为N.如图,利用S=S梯形PANM+S△ANB-S△PMO得到S=![]() [3+(-t)](3-t)+
[3+(-t)](3-t)+![]() 33-
33-![]() (-t)(-t),然后利用S的范围确定对应t的范围;
(-t)(-t),然后利用S的范围确定对应t的范围;
(3)依题意得到t=3,则P(3,-3),讨论:当直角顶点为点O时,OP⊥OQ,易得直线OQ的解析式为y=x,则解方程组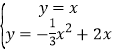
得此时点Q的坐标;当直角顶点为点P时,过点P作直线的垂线交抛物线于点Q,则可设直线PQ的解析式为y=x+b,接着把P(3,-3)代入求出b得到直线PQ的解析式为y=x-6,然后解方程组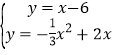 得此时Q点坐标.
得此时Q点坐标.
解:(1)∵点B与O(0,0)关于x=3对称,
∴点B坐标为(6,0),
把B(6,0)代入y=ax2+2x得36a+12=0,解得a=﹣![]() ,
,
∴抛物线解析式为y=﹣![]() x2+2x;
x2+2x;
∵y=﹣![]() x2+2x=﹣
x2+2x=﹣![]() (x﹣3)2+3,
(x﹣3)2+3,
∴顶点A的坐标为(3,3),
设直线AB解析式为y=kx+b.
把A(3,3),B(6,0)代入得![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=﹣x+6;
(2)∵直线∥AB且过点O,
∴直线解析式为y=﹣x,
设P点坐标为(t,﹣t),
当点P在第四象限时(t>0),
S=S△AOB+S△POB=![]() 63+
63+![]() 6|﹣t|=9+3t,
6|﹣t|=9+3t,
∵0<S≤18,
∴0<9+3t≤18,解得﹣3<t≤3.
又t>0,
∴0<t≤3;
当点P在第二象限时(t<0),
作PM⊥x轴于M,设对称轴与x轴交点为N.如图,
S=S梯形PANM+S△ANB﹣S△PMO![]() [3+(﹣t)](3﹣t)+
[3+(﹣t)](3﹣t)+![]() 33﹣
33﹣![]() (﹣t)(﹣t)
(﹣t)(﹣t)
=﹣3t+9,
∵0<S≤18,
∴0<﹣3+9≤18,解得﹣3≤t<3.
又t<0,
∴﹣3≤t<0;
综上所述,t的取值范围是﹣3≤t<0或0<t≤3;
(3)存在.
依题意可知,t=3,则P(3,﹣3)
当直角顶点为点O时,OP⊥OQ,
∴直线OQ的解析式为y=x,
解方程组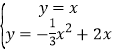 得
得![]() 或
或![]() ,此时点Q的坐标为(3,3);
,此时点Q的坐标为(3,3);
当直角顶点为点P时,过点P作直线的垂线交抛物线于点Q,
设直线PQ的解析式为y=x+b,
把P(3,﹣3)代入得b=﹣6,
∴直线PQ的解析式为y=x﹣6,
解方程组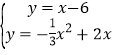 得
得![]() 或
或![]() ,此时Q点坐标为(6,0)或(﹣3,﹣9),
,此时Q点坐标为(6,0)或(﹣3,﹣9),
综上所述,点Q的坐标为(3,3)或(6,0)或(﹣3,﹣9).

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案